The Casimer Effect is a physical force arising
from a quantized field, for example between two uncharged
plates. This can produce a locally mass-negative region of
space-time that could stabilize a wormhole to allow faster than
light travel.
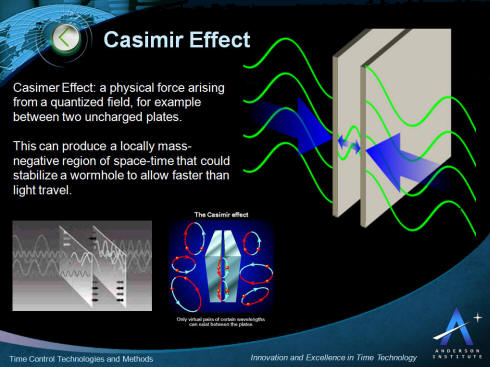
In quantum field theory, the Casimir effect and the Casimir-Polder
force are physical forces arising from a quantized field. The
typical example is of two uncharged metallic plates in a vacuum,
placed a few micrometers apart, without any external
electromagnetic field. In a classical description, the lack of
an external field also means that there is no field between the
plates, and no force would be measured between them. When this
field is instead studied using quantum electrodynamics, it is
seen that the plates do affect the virtual photons which
constitute the field, and generate a net force—either an
attraction or a repulsion depending on the specific arrangement
of the two plates.
The key characteristics of the application of the Casimir Effect
for time control and time travel are presented in the picture
below. This is followed by more detail describing the effect
below.

Although the Casimir effect can be expressed in terms of virtual
particles interacting with the objects, it is best described and
more easily calculated in terms of the zero-point energy of a
quantized field in the intervening space between the objects.
This force has been measured, and is a striking example of an
effect purely due to second quantization. However, the treatment
of boundary conditions in these calculations has led to some
controversy. In fact "Casimir's original goal was to compute the
van der Waals force between polarizable molecules" of the
metallic plates. Thus it can be interpreted without any
reference to the zero-point energy (vacuum energy) or virtual
particles of quantum fields.
Dutch physicists Hendrik B. G. Casimir and Dirk Polder proposed
the existence of the force and formulated an experiment to
detect it in 1948 while participating in research at Philips
Research Labs. The classic form of the experiment, described
above, successfully demonstrated the force to within 15% of the
value predicted by the theory.
Because the strength of the force falls off rapidly with
distance, it is only measurable when the distance between the
objects is extremely small. On a submicrometre scale, this force
becomes so strong that it becomes the dominant force between
uncharged conductors. In fact, at separations of 10 nm—about 100
times the typical size of an atom—the Casimir effect produces
the equivalent of 1 atmosphere of pressure (101.3 kPa), the
precise value depending on surface geometry and other factors.
In modern theoretical physics, the Casimir effect plays an
important role in the chiral bag model of the nucleon; and in
applied physics, it is significant in some aspects of emerging
microtechnologies and nanotechnologies.
Vacuum energy
The causes of the Casimir effect are described by quantum field
theory, which states that all of the various fundamental fields,
such as the electromagnetic field, must be quantized at each and
every point in space. In a simplified view, a "field" in physics
may be envisioned as if space were filled with interconnected
vibrating balls and springs, and the strength of the field can
be visualized as the displacement of a ball from its rest
position.
Vibrations in this field propagate and are governed by
the appropriate wave equation for the particular field in
question.
The second quantization of quantum field theory
requires that each such ball-spring combination be quantized,
that is, that the strength of the field be quantized at each
point in space. Canonically, the field at each point in space is
a simple harmonic oscillator, and its quantization places a
quantum harmonic oscillator at each point. Excitations of the
field correspond to the elementary particles of particle
physics. However, even the vacuum has a vastly complex
structure, all calculations of quantum field theory must be made
in relation to this model of the vacuum.
The vacuum has, implicitly, all of the properties that a
particle may have: spin, or polarization in the case of light,
energy, and so on. On average, all of these properties cancel
out: the vacuum is, after all, "empty" in this sense. One
important exception is the vacuum energy or the vacuum
expectation value of the energy. The quantization of a simple
harmonic oscillator states that the lowest possible energy or
zero-point energy that such an oscillator may have is
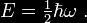
Summing over all possible oscillators at all points in space
gives an infinite quantity. To remove this infinity, one may
argue that only differences in energy are physically measurable;
this argument is the underpinning of the theory of
renormalization. In all practical calculations, this is how the
infinity is always handled. In a deeper sense, however,
renormalization is unsatisfying, and the removal of this
infinity presents a challenge in the search for a Theory of
Everything. Currently there is no compelling explanation for how
this infinity should be treated as essentially zero; a non-zero
value is essentially the cosmological constant and any large
value causes trouble in cosmology.
The Casimir
Effect
Simulation of Casimir Force |
Casimir's observation was that the second-quantized quantum
electromagnetic field, in the presence of bulk bodies such as
metals or dielectrics, must obey the same boundary conditions
that the classical electromagnetic field must obey. In
particular, this affects the calculation of the vacuum energy in
the presence of a conductor or dielectric.
Consider, for example, the calculation of the vacuum expectation
value of the electromagnetic field inside a metal cavity, such
as, for example, a radar cavity or a microwave waveguide. In
this case, the correct way to find the zero point energy of the
field is to sum the energies of the standing waves of the
cavity. To each and every possible standing wave corresponds an
energy; say the energy of the nth standing wave is En. The
vacuum expectation value of the energy of the electromagnetic
field in the cavity is then
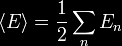
with the sum running over all possible values of n
enumerating the standing waves. The factor of 1/2 corresponds to
the fact that the zero-point energies are being summed (it is
the same 1/2 as appears in the equation
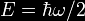 ).
Written in this way, this sum is clearly divergent; however, it
can be used to create finite expressions. ).
Written in this way, this sum is clearly divergent; however, it
can be used to create finite expressions.
In particular, one may ask how the zero point energy depends on
the shape s of the cavity. Each energy level
En
depends on the shape, and so one should write
En(s)
for the energy level, and
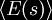 for
the vacuum expectation value. At this point comes an important
observation: the force at point p on the wall of the
cavity is equal to the change in the vacuum energy if the shape
s of the wall is perturbed a little bit, say by
δs,
at point p. That is, one has for
the vacuum expectation value. At this point comes an important
observation: the force at point p on the wall of the
cavity is equal to the change in the vacuum energy if the shape
s of the wall is perturbed a little bit, say by
δs,
at point p. That is, one has
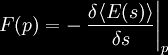
This value is finite in many practical calculations.
Casimir's calculation
In the original
calculation done by Casimir, he considered the space between a
pair of conducting metal plates at distance
a
apart. In this case, the standing waves are particularly easy to
calculate, since the transverse component of the electric field
and the normal component of the magnetic field must vanish on
the surface of a conductor. Assuming the parallel plates lie in
the x-y plane, the standing waves are
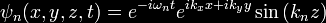
where
ψ
stands for the electric component of the electromagnetic field,
and, for brevity, the polarization and the magnetic components
are ignored here. Here,
kx
and
ky
are the wave vectors in directions parallel to the plates, and
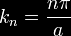
is the
wave-vector perpendicular to the plates. Here, n is an
integer, resulting from the requirement that ψ vanish on the
metal plates. The energy of this wave is
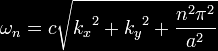
where c
is the speed of light. The vacuum energy is then the sum over
all possible excitation modes
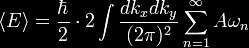
where A
is the area of the metal plates, and a factor of 2 is introduced
for the two possible polarizations of the wave. This expression
is clearly infinite, and to proceed with the calculation, it is
convenient to introduce a regulator (discussed in greater detail
below). The regulator will serve to make the expression finite,
and in the end will be removed. The zeta-regulated version of
the energy per unit-area of the plate is
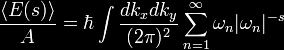
In the end, the
limit
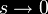 is
to be taken. Here s is just a complex number, not to be
confused with the shape discussed previously. This integral/sum
is finite for s real and larger than 3. The sum has a
pole at s=3, but may be analytically continued to s=0,
where the expression is finite. Expanding this, one gets is
to be taken. Here s is just a complex number, not to be
confused with the shape discussed previously. This integral/sum
is finite for s real and larger than 3. The sum has a
pole at s=3, but may be analytically continued to s=0,
where the expression is finite. Expanding this, one gets
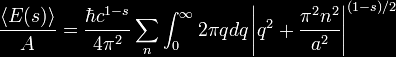
where polar
coordinates
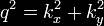 were
introduced to turn the double integral into a single integral.
The
q
in front is the Jacobian, and the
2π
comes from the angular integration. The integral is easily
performed, resulting in were
introduced to turn the double integral into a single integral.
The
q
in front is the Jacobian, and the
2π
comes from the angular integration. The integral is easily
performed, resulting in
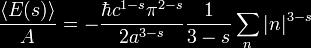
The sum may be
understood to be the Riemann zeta function, and so one has
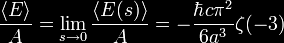
But
ζ( − 3) = 1 / 120
and so one obtains
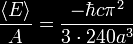
The Casimir
force per unit area
Fc
/ A
for idealized, perfectly conducting plates with vacuum between
them is
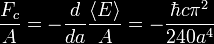
where
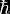 (hbar,
ħ) is the reduced Planck constant, (hbar,
ħ) is the reduced Planck constant,
c
is the speed of light,
a
is the distance between the two plates.
The force is
negative, indicating that the force is attractive: by moving the
two plates closer together, the energy is lowered. The presence
of
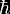 shows
that the Casimir force per unit area
Fc
/ A
is very small, and that furthermore, the force is inherently of
quantum-mechanical origin. shows
that the Casimir force per unit area
Fc
/ A
is very small, and that furthermore, the force is inherently of
quantum-mechanical origin.
More
recent theory

Concept of zero-point energy module
using the Casimir Effect |
A very complete
analysis of the Casimir effect at short distances is based upon
a detailed analysis of the van der Waals force by Lifshitz.
Using this approach, complications of the bounding surfaces,
such as the modifications to the Casimir force due to finite
conductivity, can be calculated numerically using the tabulated
complex dielectric functions of the bounding materials. In
addition to these factors, complications arise due to surface
roughness of the boundary and to geometry effects such as degree
of parallelism of bounding plates. For
boundaries at large separations, retardation effects give rise
to a long-range interaction. For the case of two parallel plates
composed of ideal metals in vacuum, the results reduce to
Casimir’s.
Measurement
One of the
first experimental tests was conducted by Marcus Sparnaay at
Philips in Eindhoven, in 1958, in a delicate and difficult
experiment with parallel plates, obtaining results not in
contradiction with the Casimir theory, but with large
experimental errors.
The Casimir
effect was measured more accurately in 1997 by Steve K.
Lamoreaux of Los Alamos National Laboratory and by Umar Mohideen
and Anushree Roy of the University of California at Riverside.
In practice, rather than using two parallel plates, which would
require phenomenally accurate alignment to ensure they were
parallel, the experiments use one plate that is flat and another
plate that is a part of a sphere with a large radius. In 2001, a
group at the University of Padua finally succeeded in measuring
the Casimir force between parallel plates using microresonators.
Regularisation
In order to be
able to perform calculations in the general case, it is
convenient to introduce a regulator in the summations. This is
an artificial device, used to make the sums finite so that they
can be more easily manipulated, followed by the taking of a
limit so as to remove the regulator.
The heat kernel
or exponentially regulated sum is
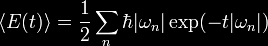
where the limit
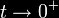 is
taken in the end. The divergence of the sum is typically
manifested as is
taken in the end. The divergence of the sum is typically
manifested as
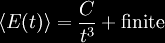
for
three-dimensional cavities. The infinite part of the sum is
associated with the bulk constant C which does not
depend on the shape of the cavity. The interesting part of the
sum is the finite part, which is shape-dependent. The Gaussian
regulator
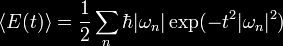
is better
suited to numerical calculations because of its superior
convergence properties, but is more difficult to use in
theoretical calculations. Other, suitably smooth, regulators may
be used as well. The zeta function regulator
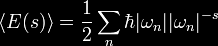
is completely
unsuited for numerical calculations, but is quite useful in
theoretical calculations. In particular, divergences show up as
poles in the complex s plane, with the bulk divergence at
s=4. This sum may be analytically continued past this
pole, to obtain a finite part at s=0.
Not every cavity configuration necessarily leads to a finite
part (the lack of a pole at s=0) or shape-independent
infinite parts. In this case, it should be understood that
additional physics has to be taken into account. In particular,
at extremely large frequencies (above the plasma frequency),
metals become transparent to photons (such as x-rays), and
dielectrics show a frequency-dependent cutoff as well. This
frequency dependence acts as a natural regulator. There are a
variety of bulk effects in solid state physics, mathematically
very similar to the Casimir effect, where the cutoff frequency
comes into explicit play to keep expressions finite. (These are
discussed in greater detail in Landau and Lifshitz,
"Theory of Continuous Media".)
Generalities
experimental setup for the conversion of
vacuum energy into mechanical-energy. |
The Casimir effect
can also be computed using the mathematical mechanisms of
functional integrals of quantum field theory, although such
calculations are considerably more abstract, and thus difficult
to comprehend. In addition, they can be carried out only for the
simplest of geometries. However, the formalism of quantum field
theory makes it clear that the vacuum expectation value
summations are in a certain sense summations over so-called
"virtual particles". More
interesting is the understanding that the sums over the energies
of standing waves should be formally understood as sums over the
eigenvalues of a Hamiltonian. This allows atomic and molecular
effects, such as the van der Waals force, to be understood as a
variation on the theme of the Casimir effect. Thus one considers
the Hamiltonian of a system as a function of the arrangement of
objects, such as atoms, in configuration space. The change in
the zero-point energy as a function of changes of the
configuration can be understood to result in forces acting
between the objects.
In
the chiral bag model of the nucleon, the Casimir energy plays an
important role in showing the mass of the nucleon is independent
of the bag radius. In addition, the spectral asymmetry is
interpreted as a non-zero vacuum expectation value of the baryon
number, cancelling the topological winding number of the pion
field surrounding the nucleon.
Casimir effect and
wormholes
Exotic matter with
negative energy density is required to stabilize a wormhole.
Morris, Thorne and Yurtsever pointed out that the quantum
mechanics of the Casimir effect can be used to produce a locally
mass-negative region of space-time, and suggested that negative
effect could be used to stabilize a wormhole to allow faster
than light travel. This concept has been used extensively in
Science Fiction.
Analogies
A similar analysis
can be used to explain Hawking radiation that causes the slow
"evaporation" of black holes (although this is generally
visualized as the escape of one particle from a virtual
particle-antiparticle pair, the other particle having been
captured by the black hole).
Repulsive
forces
There are few
instances wherein the Casimir effect can give rise to repulsive
forces between uncharged objects. In a seminal paper, Evgeny
Lifshitz showed (theoretically) that in certain circumstances
(most commonly involving liquids), repulsive forces can arise.
This has sparked interest in applications of the Casimir effect
toward the development of levitating devices. Other scientists
have also suggested the use of gain media to achieve a similar
levitation effect, though this is controversial because these
materials seem to violate fundamental causality constraints and
the requirement of thermodynamic equilibrium. An experimental
demonstration of the Casimir-based levitation was recently
demonstrated by the Capasso group at Harvard through experiments
involving a gold-coated particle and silica thin film immersed
in bromobenzene.
Applications
It has been
suggested that the
Casimir forces have application in
nanotechnology, in particular silicon integrated circuit
technology based micro- and nanoelectromechanical systems, and
so-called Casimir
oscillators.
Classical
'Critical' Casimir Effect
In 2008,
physicists in Germany made the first direct measurements of the
“critical Casimir effect”, a classical analogue of the quantum
Casimir effect. This effect had been theoretically predicted in
1978 by Michael Fisher and Pierre-Gilles de Gennes but all
observations had been indirect.
In this
experiment, the critical Casimir effect arises in a mixed liquid
that is close to its critical point. The liquid used was a
solution of water and the oil 2,6-lutidine which has a critical
point of 34°C at normal atmospheric pressure. As this liquid
approaches its critical point, the oil and water starts separate
into small regions whose size and shape are subject to
statistical fluctuations and that exhibit random Brownian
motion. To demonstrate the effect, a tiny coated Styrofoam ball
is suspended in the liquid close to the wall of its coated glass
container. The ball and the container coatings are the same and
both have a preference for either oil or water. As the liquid
nears its critical point, total internal reflection microscopy
is used to detect displacements of the ball. From the sudden
movements detected only towards the glass, the classical Casimir
force was calculated to be approximately 600 fN (6 x 10−13
N). To tune the effect for repulsion, the coatings of the glass
and the ball are changed so that one prefers oil and the other
water.
While the German
physicists say this reverse critical Casimir effect could be
useful in nanoelectromechanical systems, its dependence upon a
very specific temperature presently limits its usefulness.
|
|
|
