Quantum Tunneling is an evanescent wave coupling effect that occurs
in quantum mechanics. The correct wavelength combined with the proper
tunneling barrier makes it possible to pass signals faster than
light, backwards in time.
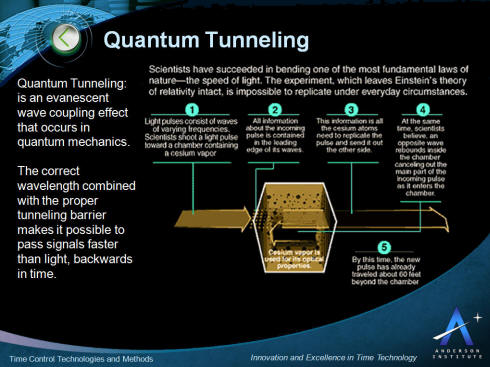
In the diagram above light pulses consisting of waves of various
frequencies are shot toward a 10 centimeter chamber containing
cesium vapor. All information about the incoming pulse is
contained in the leading edge of its waves. This information is
all the cesium atoms need to replicate the pulse and send it out
the other side.
At the same time it is believed an opposite wave rebounds inside
the chamber cancelling out the main part of the incoming pulse
as it enters the chamber. By this time the new pulse, moving
faster than the speed of light, has traveled about 60 feet
beyond the chamber. Essentially the pulse has left the chamber
before it finished entering, traveling backwards in time.
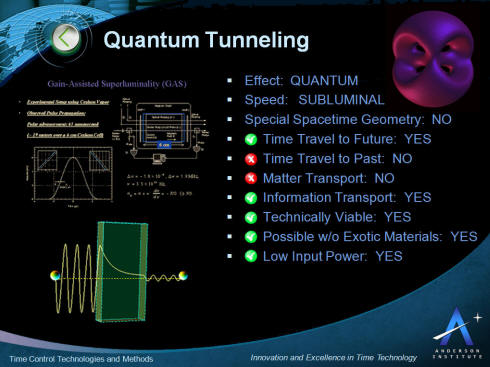
The key characteristics of the application of quantum tunneling
for time control and time travel are presented in the picture
below. This is followed by more detail describing the phenomenon
below.
Wave-mechanical tunneling (also called quantum-mechanical
tunneling, quantum tunneling, and the tunnel effect) is an
evanescent wave coupling effect that occurs in the context of
quantum mechanics because the behavior of particles is governed
by Schrödinger's wave-equation. All wave equations exhibit
evanescent wave coupling effects if the conditions are right.
Wave coupling effects mathematically equivalent to those called
"tunneling" in quantum mechanics can occur with Maxwell's
wave-equation (both with light and with microwaves), and with
the common non-dispersive wave-equation often applied (for
example) to waves on strings and to acoustics.
For these effects to occur there must be a situation where a
thin region of "medium type 2" is sandwiched between two regions
of "medium type 1", and the properties of these media have to be
such that the wave equation has "traveling-wave" solutions in
medium type 1, but "real exponential solutions" (rising and
falling) in medium type 2. In optics, medium type 1 might be
glass, medium type 2 might be vacuum. In quantum mechanics, in
connection with motion of a particle, medium type 1 is a region
of space where the particle total energy is greater than its
potential energy, medium type 2 is a region of space (known as
the "barrier") where the particle total energy is less than its
potential energy.
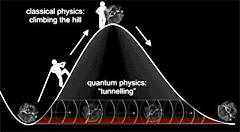
If conditions are right, amplitude from a traveling wave,
incident on medium type 2 from medium type 1, can "leak through"
medium type 2 and emerge as a traveling wave in the second
region of medium type 1 on the far side. If the second region of
medium type 1 is not present, then the traveling wave incident
on medium type 2 is totally reflected, although it does
penetrate into medium type 2 to some extent. Depending on the
wave equation being used, the leaked amplitude is interpreted
physically as traveling energy or as a traveling particle, and,
numerically, the ratio of the square of the leaked amplitude to
the square of the incident amplitude gives the proportion of
incident energy transmitted out the far side, or (in the case of
the Schrödinger equation) the probability that the particle
"tunnels" through the barrier.
Quantum Tunneling Introduction
Quantum Tunneling |
The scale on which these "tunneling-like phenomena" occur
depends on the wavelength of the traveling wave. For electrons
the thickness of "medium type 2" (called in this context "the
tunneling barrier") is typically a few nanometers; for
alpha-particles tunneling out of a nucleus the thickness is
very much less; for the analogous phenomenon involving light the
thickness is very much greater.
With Schrödinger's wave-equation, the characteristic that
defines the two media discussed above is the kinetic energy of
the particle if it is considered as an object that could be
located at a point. In medium type 1 the kinetic energy would be
positive, in medium type 2 the kinetic energy would be negative.
There is no inconsistency in this, because particles cannot
physically be located at a point: they are always spread out ("delocalized")
to some extent, and the kinetic energy of the delocalized object
is always positive.
What is true is that it is sometimes mathematically convenient
to treat particles as behaving like points, particular in the
context of Newton's Second Law and classical mechanics
generally. In the past, people thought that the success of
classical mechanics meant that particles could always and in all
circumstances be treated as if they were located at points. But
there never was any convincing experimental evidence that this
was true when very small objects and very small distances are
involved, and we now know that this viewpoint was mistaken.
However, because it is still traditional to teach students early
in their careers that particles behave like points, it sometimes
comes as a big surprise for people to discover that it is well
established that traveling physical particles always physically
obey a wave-equation (even when it is convenient to use the
mathematics of moving points). Clearly, a hypothetical classical
point particle analyzed according to Newton's Laws could not
enter a region where its kinetic energy would be negative. But,
a real delocalized object, that obeys a wave-equation and always
has positive kinetic energy, can leak through such a region if
conditions are right. An approach to tunneling that avoids
mention of the concept of "negative kinetic energy" is set out
below in the section on "Schrödinger equation tunneling
basics".
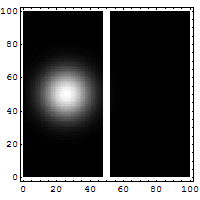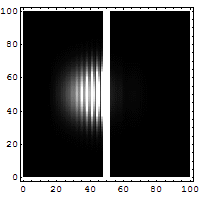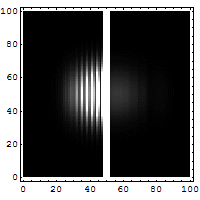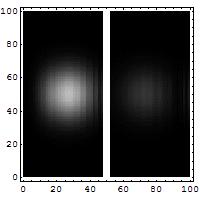
Reflection and tunneling of an
electron
wave packet directed at a potential barrier.
The
bright spot moving to the left is the
reflected part of
the wave packet. A very
dim spot can be seen moving to
the right
of the barrier. This is the small fraction of
the wave packet that tunnels through the
classically
forbidden barrier. Also notice
the interference fringes
between the
incoming and reflected waves.
|
An electron approaching a barrier has to be represented as a
wave-train. This wave-train can sometimes be quite long –
electrons in some materials can be 10 to 20 nm long. This makes
animations difficult. If it were legitimate to represent the
electron by a short wave-train, then tunneling could be
represented as in the animation alongside.
It is sometimes said that tunneling occurs only in quantum
mechanics. Unfortunately, this statement is a bit of linguistic
conjuring trick. As indicated above, "tunneling-type"
evanescent-wave phenomena occur in other contexts too. But,
until recently, it has only been in quantum mechanics that
evanescent wave coupling has been called "tunneling". (However,
there is an increasing tendency to use the label "tunneling" in
other contexts too, and the names "photon tunneling" and
"acoustic tunneling" are now used in the research literature.)
With regards to the mathematics of tunneling, a special problem
arises. For simple tunneling-barrier models, such as the
rectangular barrier, the Schrödinger equation can be solved
exactly to give the value of the tunneling probability
(sometimes called the "transmission coefficient"). Calculations
of this kind make the general physical nature of tunneling
clear. One would also like to be able to calculate exact
tunneling probabilities for barrier models that are physically
more realistic. However, when appropriate mathematical
descriptions of barriers are put into the Schrödinger equation,
then the result is an awkward non-linear differential equation.
Usually, the equation is of a type where it is known to be
mathematically impossible in principle to solve the equation
exactly in terms of the usual functions of mathematical physics,
or in any other simple way. Mathematicians and mathematical
physicists have been working on this problem since at least
1813, and have been able to develop special methods for solving
equations of this kind approximately. In physics these are known
as "semi-classical" or "quasi-classical" methods. A common
semi-classical method is the so-called WKB approximation (also
known as the "JWKB approximation"). The first known attempt to
use such methods to solve a tunneling problem in physics was
made in 1928, in the context of field electron emission. It is
sometimes considered that the first people to get the
mathematics of applying this kind of approximation to tunneling
fully correct (and to give reasonable mathematical proof that
they had done so) were N. Fröman and P.O. Fröman, in 1965. Their
complex ideas have not yet made it into theoretical-physics
textbooks, which tend to give simpler (but slightly more
approximate) versions of the theory. An outline of one
particular semi-classical method is given below.
Three notes may be helpful. In general, students taking physics
courses in quantum mechanics are presented with problems (such
as the quantum mechanics of the hydrogen atom) for which exact
mathematical solutions to the Schrödinger equation exist.
Tunneling through a realistic barrier is a reasonably basic
physical phenomenon. So it is sometimes the first problem that
students encounter where it is mathematically impossible in
principle to solve the Schrödinger equation exactly in any
simple way. Thus, it may also be the first occasion on which
they encounter the "semi-classical-method" mathematics needed to
solve the Schrödinger equation approximately for such problems.
Not surprisingly, this mathematics is likely to be unfamiliar,
and may feel "odd". Unfortunately, it also comes in several
different variants, which doesn't help.
Also, some accounts of tunneling seem to be written from a
philosophical viewpoint that a particle is "really" point-like,
and just has wave-like behavior. There is very little
experimental evidence to support this viewpoint. A preferable
philosophical viewpoint is that the particle is "really"
delocalized and wave-like, and always exhibits wave-like
behavior, but that in some circumstances it is convenient to
use the mathematics of moving points to describe its motion.
This second viewpoint is used in this section. The precise
nature of this wave-like behavior is, however, a much deeper
matter, beyond the scope of this article on tunneling.
Although the phenomenon under discussion here is usually called
"quantum tunneling" or "quantum-mechanical
tunneling", it is
the wave-like aspects of particle behavior that are important
in tunneling theory, rather than effects relating to the
quantization of the particle's energy states. For this reason,
some writers prefer to call the phenomenon "wave-mechanical
tunneling.
History
By 1928, George Gamow had solved the theory of the alpha decay
of a nucleus via tunneling. Classically, the particle is
confined to the nucleus because of the high energy requirement
to escape the very strong potential. Under this system, it takes
an enormous amount of energy to pull apart the nucleus. In
quantum mechanics, however, there is a probability the particle
can tunnel through the potential and escape. Gamow solved a
model potential for the nucleus and derived a relationship
between the half-life of the particle and the energy of the
emission.
Alpha decay via tunneling was also solved concurrently by
Ronald Gurney and Edward Condon. Shortly thereafter, both groups
considered whether particles could also tunnel into the nucleus.
After attending a seminar by Gamow, Max Born recognized the
generality of quantum-mechanical tunneling. He realized that
the tunneling phenomenon was not restricted to nuclear physics,
but was a general result of quantum mechanics that applies to
many different systems. Today the theory of tunneling is even
applied to the early cosmology of the universe.
Quantum tunneling was later applied to other situations, such
as the cold emission of electrons, and perhaps most importantly
semiconductor and superconductor physics. Phenomena such as
field emission, important to flash memory, are explained by
quantum tunneling. Tunneling is a source of major current
leakage in Very-large-scale integration (VLSI) electronics, and
results in the substantial power drain and heating effects that
plague high-speed and mobile technology.
Another major application is in electron-tunneling microscopes
which can resolve objects that are too small to see using
conventional microscopes. Electron tunneling microscopes
overcome the limiting effects of conventional microscopes
(optical aberrations, wavelength limitations) by scanning the
surface of an object with tunneling electrons.
Quantum tunneling has been shown to be a mechanism used by
enzymes to enhance reaction rates. It has been demonstrated that
enzymes use tunneling to transfer both electrons and nuclei
such as hydrogen and deuterium. It has even been shown, in the
enzyme glucose oxidase, that oxygen nuclei can tunnel under
physiological conditions. |
|
|
