Philosophical Approach to Time

A Philosophical Approach to Time

An article by Bradley Dowden, California State University, Sacramento

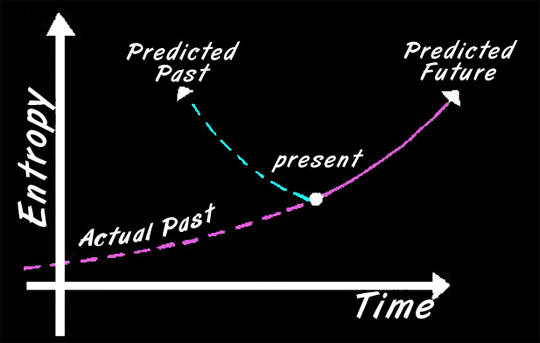
Time has been studied by philosophers and scientists for 2,500 years, and thanks to this attention it is much better understood today. Nevertheless, many issues remain to be resolved. Here is a short list of the most important ones—what time actually is; whether time exists when nothing is changing; what kinds of time travel are possible; why time has an arrow; whether the future and past are real; how to analyze the metaphor of time’s flow; whether future time will be infinite; whether there was time before the Big Bang; whether tensed or tenseless concepts are semantically basic; what is the proper formalism or logic for capturing the special role that time plays in reasoning; and what are the neural mechanisms that account for our experience of time. Some of these issues will be resolved by scientific advances alone, but others require philosophical analysis.

Consider this one issue upon which philosophers of time are deeply divided: What sort of ontological differences are there among the present, past and future? There are three competing theories. Presentists argue that necessarily only present objects and present experiences are real, and we conscious beings recognize this in the special “vividness” of our present experience. The dinosaurs have slipped out of reality. According to the growing-universe or growing-block theory, the past and present are both real, but the future is not because the future is indeterminate or merely potential. Dinosaurs are real, but our death is not. The third and more popular theory is that there are no significant ontological differences among present, past, and future because the differences are merely subjective. This view is called “the block universe theory” or “eternalism.”

That controversy raises the issue of tenseless versus tensed theories of time. The block universe theory implies a tenseless theory. The earliest version of this theory implied that tensed terminology can be removed and replaced with tenseless terminology. For example, the future-tensed sentence, “The Lakers will win the basketball game” might be analyzed as, “The Lakers do win at time t, and time t happens after the time of this utterance.” The future tense has been removed, and the new verb phrases “do win” and “happens after” are tenseless logically, although they are grammatically in the present tense. Advocates of a tensed theory of time object to this strategy and say that tenseless terminology is not semantically basic but should be analyzed in tensed terms, and that tensed facts are needed to make the tensed statements be true. For example, a tensed theory might imply that no adequate account of the present tensed fact that it is now midnight can be given without irreducible tensed properties such as presentness or now-ness. So, the philosophical debate is over whether tensed concepts have semantical priority over untensed concepts, and whether tensed facts have ontological priority over untensed facts.

This article explores both what is now known about time and what is controversial and unresolved, by addressing the questions listed in the table of contents.

Table of Contents
1. What Should a Philosophical Theory of Time Do?
2. How is Time Related to Mind?
3. What is Time?
a. The Variety of Answers
b. Time vs. “Time”
c. Defining Time Order with Causal Order
d. Linear and Circular Time
e. Does Time Emerge from Something More Basic?
4. What does Science Require of Time?
a. Relativity and Quantum Mechanics
b. The Big Bang
c. Infinite Time
d. Atoms of Time
5. What Kinds of Time Travel are Possible?
6. Is the Relational Theory Preferable to the Absolute Theory?
7. Does Time Flow?
8. What Gives Time its Direction or “Arrow”?
a. What Needs to be Explained?
b. Explanations or Theories of the Arrow
c. Multiple Arrows
d. Reversing Time
9. Is Only the Present Real?
10. Are there Essentially Tensed Facts?
11. What is Temporal Logic?
12. Supplements
a. Frequently Asked Questions
b. Special Relativity: Proper Times, Coordinate Systems, and Lorentz Transformations
13. References and Further Reading

1. What Should a Philosophical Theory of Time Do?

Should it define the word “time”? Yes, but it is improper to demand that we define our term “time” as a prelude to saying anything more about time, in large part because, as we have learned more about time, our definition has evolved. What we really want is to build a comprehensive, philosophical theory of time that helps us understand time by solving problems about time. We do not want to start building this theory by adopting a definition of time that prejudices the project from the beginning.

Although there are theories of how to solve a specific problem about time, it is always better to knit together solutions to several problems. Ideally, the goal is to produce a theory of time that will solve in a systematic way the constellation of problems involving time. What are those problems?

One is to clarify the relationship between time and the mind. Does time exist for beings that have no minds? It is easy to confuse time itself with the perception of time.

Another problem is to decide which of our intuitions about time should be retained. Some of these intuitions may reflect deep insights into the nature of time, and others may be faulty ideas inherited from our predecessors. It is not obvious which is which. For one example, if we have the intuition that time flows, but our science implies otherwise, then which view should get priority? Philosophers of time must solve the problem of how to treat our temporal intuitions.

A third problem for a philosophical theory of time is to clarify what physical science presupposes and implies about time. A later section of this article examines this topic. Most all philosophers of time claim that philosophical theories should be consistent with physical science, or, if not, then they must accept the heavy burden of proof to justify the inconsistency.

A philosophical theory of time should describe the relationship between instants and events. Does the instant that we label as “11:01 A.M.” for a certain date exist independently of the events that occur then? In other words, can time exist if no event is happening? This question or problem raises the thorny metaphysical issue of absolute vs. relational theories of time.

A theory of time should address the question of time’s apparent direction. If the projectionist in the movie theater (cinema) shows a film of cream being added into black coffee but runs the film backwards, we in the audience can immediately tell that events could not have occurred this way. We recognize the arrow of time because we know about the one-directional processes in nature. This arrow or unidirectionality becomes less and less apparent to us viewers as the film subject gets smaller and smaller and the time interval gets shorter and shorter until finally we are viewing processes that could just as easily go the other way, at which point the arrow of time has disappeared. Philosophers disagree about the explanation of the arrow. Could it be a consequence of the laws of science? The arrow appears to be very basic for understanding nature, yet it is odd that asymmetries in time do not appear in the principal, basic dynamical laws of physics. Could the arrow of time reverse some day? Philosophers wonder what life would be like in some far off corner of the universe if the arrow of time were reversed there. Would people there walk backwards up steps while remembering the future?

Another philosophical problem about time concerns the two questions, “What is the present, and why does it move into the past?” If we know what the present is, then we ought to be able to answer the question, “How long does the present last?” Regarding the “movement” of the present into the past, many philosophers are suspicious of this notion of the flow of time, the march of time. They doubt whether it is a property of time as opposed to being some feature of human perception. Assuming time does flow, is the flow regular? If the flow is irregular, then perhaps Friday seconds last longer than Thursday seconds, as the flow of Friday time slows to a crawl, or perhaps Friday might contain more seconds than Thursday.

Are there ontological differences among the past, present, and future? Some philosophers doubt whether the future and past are as real as the present, the feature that is referred to by the word “now.” A famous philosophical argument says that, if the future were real, then it would be fixed now, and we would not have the freedom to affect that future. Since we do have that freedom, the future can not be real. Some philosophers consider this to be a clever, but faulty argument.

For a last example of a philosophical issue regarding time, is time a fundamental feature of nature, or does it emerge from more basic features–in analogy to the way the smoothness of water flow emerges from the complicated behavior of the underlying molecules? From what more basic feature does time emerge?

A full theory of time should address this constellation of philosophical issues about time. Narrower theories of time will focus on resolving a few members of this constellation, but the long-range goal is to knit together these theories into a full, systematic, detailed theory of time.

2. How is Time Related to Mind?

Physical time is public time, the time that clocks are designed to measure. Psychological time or phenomenological time is private time. It is perhaps best understood as awareness of physical time. Psychological time passes swiftly for us while we are enjoying reading a book, but it slows dramatically if we are waiting anxiously for the water to boil on the stove. The slowness is probably due to focusing our attention on short intervals of physical time. Meanwhile, the clock by the stove is measuring physical time and is not affected by anybody’s awareness.

When a physicist defines speed to be the rate of change of position with respect to time, the term “time” refers to physical time. Physical time is more basic for helping us understand our shared experiences in the world, and so it is more useful than psychological time for doing science. But psychological time is vitally important for understanding many human thought processes. We have an awareness of the passage of time even during our sleep, and we awake knowing we have slept for one night, not for one month. But if we have been under a general anesthetic or have been knocked unconscious and then wake up, we may have no sense of how long we have been unconscious. Psychological time stopped. Some philosophers claim that psychological time is completely transcended in the mental state called “nirvana.”

Within the field of cognitive science, one wants to know what are the neural mechanisms that account not only for our experience of time’s flow, but also for our ability to place events into the proper time order. See (Damasio, 2006) for further discussion of the progress in this area of cognitive science. The most surprising scientific discovery about psychological time is Benjamin Libet’s experiments in the 1970s that show, or so it is claimed, that the brain events involved in initiating free choices occur about a third of a second before we are aware of our choice. Before Libet’s work, it was universally agreed that a person is aware of deciding to act freely, then later the body initiates the action.

Psychologists are interested in whether we can speed up our minds relative to physical time. If so, we might become mentally more productive, get more high quality decision making done per fixed amount of physical time, learn more per minute. Several avenues have been explored: using drugs such as cocaine and amphetamines, undergoing extreme experiences such as jumping backwards off a tall tower with bungee cords attached to the legs, and trying different forms of meditation. So far, none of these avenues have led to success productivity-wise.

Any organism’s sense of time is subjective, but is the time that is sensed also subjective, a mind-dependent phenomenon? Without minds in the world, nothing in the world would be surprising or beautiful or interesting. Can we add that nothing would be in time? If judgments of time were subjective in the way judgments of being interesting vs. not-interesting are subjective, then it would be miraculous that everyone can so easily agree on the ordering of public events in time. For example, first, Einstein was born, then he went to school, then he died. Everybody agrees that it happened in this order: birth, school, death. No other order. The agreement on time order for so many events is part of the reason that most philosophers and scientists believe physical time is an objective phenomenon not dependent on being consciously experienced. The other part of the reason time is believed to be objective is that our universe has a large number of different processes that bear consistent time relations, or frequency of occurrence relations, to each other. For example, the frequency of a fixed-length pendulum is a constant multiple of the half life of a specific radioactive uranium isotope; the relationship does not change as time goes by (at least not much and not for a long time). The existence of these sorts of relationships makes our system of physical laws much simpler than it otherwise would be, and it makes us more confident that there is something objective we are referring to with the time-variable in those laws. The stability of these relationships over a long time also make it easy to create clocks. Time can be measured easily because we have access to long term simple harmonic oscillators that have a regular period or “regular ticking.” This regular motion shows up in completely different stable systems when they are disturbed: a ball swinging from a string (a pendulum), a ball bouncing up and down from a coiled spring, a planet orbiting the sun, organ pipes, electric circuits, and atoms in a crystal lattice. Many of these systems make good clocks.

Aristotle raised this issue of the mind-dependence of time when he said, “Whether, if soul (mind) did not exist, time would exist or not, is a question that may fairly be asked; for if there cannot be someone to count there cannot be anything that can be counted…” [Physics, chapter 14]. He does not answer his own question because, he says rather profoundly, it depends on whether time is the conscious numbering of movement or instead is just the capability of movements being numbered were consciousness to exist.

St. Augustine, adopting a subjective view of time, said time is nothing in reality but exists only in the mind’s apprehension of that reality. In the 11th century, the Persian philosopher Avicenna doubted the existence of physical time, arguing that time exists only in the mind due to memory and expectation. The 13th century philosophers Henry of Ghent and Giles of Rome said time exists in reality as a mind-independent continuum, but is distinguished into earlier and later parts only by the mind. In the 13th century, Duns Scotus clearly recognized both physical and psychological time.

At the end of the 18th century, Kant suggested a subtle relationship between time and mind–that our mind actually structures our perceptions so that we can know a priori that time is like a mathematical line. Time is, on this theory, a form of conscious experience, and our sense of time is a necessary condition of our experience. In the 19th century, Ernst Mach claimed instead that our sense of time is a simple sensation. This controversy took another turn when other philosophers argued that both Kant and Mach were incorrect because our sense of time is an intellectual construction (see Whitrow, p. 64).

In the 20th century, the philosopher of science Bas van Fraassen described physical time by saying, “There would be no time were there no beings capable of reason” just as “there would be no food were there no organisms, and no teacups if there were no tea drinkers,” and no cultural objects without a culture.

The controversy in metaphysics between idealism and realism is that, for the idealist, nothing exists independently of the mind. If this controversy is settled in favor of idealism, then time, too, would have that subjective feature–physical time as well as psychological time.

It has been suggested by some philosophers that Einstein’s theory of relativity, when confirmed, showed us that time depends on the observer, and thus that time is subjective, or dependent on the mind. This error is probably caused by Einstein’s use of the term “observer.” Einstein’s theory does imply that the duration of an event is not absolute but depends on the observer’s frame of reference or coordinate system. But what Einstein means by “observer’s frame of reference” is merely a perspective or framework from which measurements could be made. The “observer” does not have to be a conscious being or have a mind. So, Einstein is not making a point about mind-dependence.

For more on the consciousness of time and related issues, see the article “Phenomenology and Time-Consciousness.”

3. What is Time?

a. The Variety of Answers

The most popular short answer to the question “What is physical time?” is that it is not a substance or object but rather a special system of relations among instantaneous events. This is the answer offered by Adolf Grünbaum who applies the contemporary mathematical theory of continuity to physical processes, and says time is a linear continuum of instants and is a distinguished one-dimensional sub-space of four-dimensional spacetime.

How do we tell whether this is the correct answer to our question? To be convinced, we need to be told what the relevant terms mean, such as “certain system of relations.” In addition, we need to be presented with a theory of time implying that time is this system of relations; and we need to be shown how that theory adequately addresses the many features that are required for a successful theory of time. Finally, we need to compare this theory to its alternatives. This article will not carry out these tasks.

A different, but popular answer to the question “What is time?” is that time is the form of becoming. To assess this answer, which is from Alfred North Whitehead, we need to be told what the term “form of becoming” means; we need to be presented with a detailed theory of time implying that time is the form of becoming; and we need to investigate how it addresses those many features required for a successful theory of time. A third answer or theory of time is Michael Dummett’s constructive model of time; he argues that time is a composition of intervals rather than of durationless instants. The model is constructive in the sense that it implies there do not exist any times which are not detectable in principle by a physical process. A fourth answer is that time is a distinguished one-dimensional sub-space of spacetime, but spacetime is a substance. This substantivalist answer is explored in a later section. There are many other ways that our question has been answered.

If physical time and psychological time are two different kinds of time, then two answers are required to the question “What is time?” and some commentary is required regarding their relationships, such as whether one is more fundamental. Many philosophers of science argue that physical time is more fundamental even though psychological time is discovered first by each of us as we grow out of our childhood, and even though psychological time was discovered first as we human beings evolved from our animal ancestors. The remainder of this article focuses more on physical time than psychological time.

Another answer to our question, “What is time?” is that time is whatever the time variable t is denoting in the best-confirmed and most fundamental theories of current science. “Time” is given an implicit definition this way. Nearly all philosophers would agree that we do learn much about physical time by looking at the behavior of the time variable in these theories; but they complain that the full nature of physical time can be revealed only with a philosophical theory of time that addresses the many philosophical issues that scientists do not concern themselves with.

Bothered by the contradictions they claimed to find in our concept of time, some philosophers, notably Zeno, Plato, Spinoza, Hegel, and McTaggart, answer the question, “What is time?” by replying that it is nothing because it does not exist. In a similar vein, the early 20th century English philosopher F. H. Bradley argues, “Time, like space, has most evidently proved not to be real, but a contradictory appearance….The problem of change defies solution.” However, most philosophers agree that time does exist. They just can not agree on what it is.

Let’s briefly explore other answers that have been given throughout history to our question, “What is time?” Aristotle claimed that “time is the measure of change” [Physics, chapter 12], but he emphasized “that time is not change [itself]” because a change “may be faster or slower, but not time…” [Physics, chapter 10]. For example, a specific change such as the descent of a leaf can be faster or slower, but time itself can not be faster or slower. In developing his views about time, Aristotle advocated what is now referred to as the relational theory when he said, “there is no time apart from change….” [Physics, chapter 11]. In addition, Aristotle said time is not discrete or atomistic but “is continuous…. In respect of size there is no minimum; for every line is divided ad infinitum. Hence it is so with time” [Physics, chapter 11].

René Descartes had a very different answer to “What is time?” He argued that a material body has the property of spatial extension but no inherent capacity for temporal endurance, and that God by his continual action sustains (or re-creates) the body at each successive instant. Time is a kind of sustenance or re-creation.

In the 17th century, the English physicist Isaac Barrow rejected Aristotle’s linkage between time and change. Barrow said time is something which exists independently of motion or change and which existed even before God created the matter in the universe. Barrow’s student, Isaac Newton, agreed that this absolute theory of time is correct. Newton argued very specifically that time and space are an infinitely large container for all events, and that the container exists with or without the events. He added that space and time are not material substances, but are like substances in not being dependent on matter or motions or anything else except God.

Gottfried Leibniz objected. He argued that time is not an entity existing independently of actual events. He insisted that Newton had underemphasized the fact that time necessarily involves an ordering of any pair of non-simultaneous events. This is why time “needs” events, so to speak. Leibniz added that this overall order is time. He accepts a relational theory of time and rejects an absolute theory.

In the 18th century, Immanuel Kant said time and space are forms that the mind projects upon the external things-in-themselves. He spoke of our mind structuring our perceptions so that space always has a Euclidean geometry, and time has the structure of the mathematical line. Kant’s idea that time is a form of apprehending phenomena is probably best taken as suggesting that we have no direct perception of time but only the ability to experience things and events in time. Some historians distinguish perceptual space from physical space and say that Kant was right about perceptual space. It is difficult, though, to get a clear concept of perceptual space. If physical space and perceptual space are the same thing, then Kant is claiming we know a priori that physical space is Euclidean. With the discovery of non-Euclidean geometries in the 1820s, and with increased doubt about the reliability of Kant’s method of transcendental proof, the view that truths about space and time are apriori truths began to lose favor.

b. Time vs. “Time”

Whatever time is, it is not “time.” One has four letters; the other does not. Nevertheless, it might help us understand time if we improved our understanding of the sense of the word “time.” Should the proper answer to the question “What is time?” produce a definition of the word as a means of capturing its sense? Definitely not–if the definition must be some analysis that provides a simple paraphrase in all its occurrences. There are just too many varied occurrences of the word: time out, behind the times, in the nick of time, and so forth.

But how about narrowing the goal to a definition of the word “time” in its main sense, the sense that most interests philosophers and physicists? That is, explore the usage of the word “time” in its principal sense as a means of learning what time is. Well, this project would require some consideration of the grammar of the word “time.” Most philosophers today would agree with A. N. Prior who remarked that, “there are genuine metaphysical problems, but I think you have to talk about grammar at least a little bit in order to solve most of them.” However, do we learn enough about what time is when we learn about the grammatical intricacies of the word? John Austin made this point in “A Plea for Excuses,” when he said, if we are using the analytic method, the method of analysis of language, in order to sharpen our perception of the phenomena, then “it is plainly preferable to investigate a field where ordinary language is rich and subtle, as it is in the pressingly practical matter of Excuses, but certainly is not in the matter, say, of Time.” Ordinary-language philosophers have studied time talk, what Wittgenstein called the “language game” of discourse about time. Wittgenstein’s expectation is that by drawing attention to ordinary ways of speaking we will be able to dissolve rather than answer our philosophical questions. But most philosophers of time are unsatisfied with this approach; they want the questions answered, not dissolved, although they are happy to have help from the ordinary language philosopher in clearing up misconceptions that may be produced by the way we use the word in our ordinary, non-technical discourse.

c. Defining Time Order with Causal Order

In 1924, Hans Reichenbach defined time order in terms of possible cause. Event A happens before event B if A could have caused B but B could not have caused A. This was the first causal theory of time, although Leibniz had said, “If of two elements which are not simultaneous one comprehends the cause of the other, then the former is considered as preceding, the latter as succeeding.” The usefulness of the causal theory depends on a clarification of the notorious notions of causality and possibility without producing a circular explanation that presupposes an understanding of time order. Reichenbach’s idea was that causal order can be explained in terms of the “fork asymmetry.” The asymmetry is due to the fact that outgoing processes from a common center tend to be correlated with one another, but incoming processes to a common center are uncorrelated. [Do you remember ever tossing a rock into a still pond? There’s a correlation among all sorts of later events such as the rock’s disappearing under the water, the water surface getting wavy, your hearing a splash sound, the water surging slightly up the bank at the edge of the pond, and even of the pond being warmer. Imagine what the initial conditions at the edge and bottom of the pond must be like to produce correlated, incoming, concentric water waves so that as they reach the center the rock flies out of the water, leaving the water surface smooth, and sound waves rush out of your ear and converge on the surface where the splash is unoccuring, and the pond is left cooler.] Some philosophers argue that temporal asymmetry, but not temporal priority, can be analyzed in terms of causation [put more simply, event A's not occuring simultaneously with B can be analyzed in terms of cause and possible cause, but what can't be analyzed in this manner is A's occuring first]. Even if Reichenbach were correct that temporal priority can be analyzed in terms of causation, the question remains whether time itself can be analyzed in those terms.

The usefulness of the causal theory also depends on a refutation of David Hume’s view that causation is simply a matter of constant conjunction [that is, event A's causing event B is simply B's always occurring if A does]. For Hume, there is nothing metaphysically deep about causes preceding their effects; it is just a matter of convention that we use the terms “cause” and “effect” to distinguish the earlier and later members of a pair of events which are related by constant conjunction.

d. Linear and Circular Time

During history, a variety of answers have been given to the question of whether time is like a line or, instead, like a circle. The concept of linear time first appeared in the writings of the Hebrews and the Zoroastrian Iranians. The Roman writer Seneca also advocated linear time. Plato and most other Greeks and Romans believed time to be motion and believed cosmic motion was cyclical, but this was not envisioned as requiring any detailed endless repetition such as the multiple rebirths of Socrates. However, the Pythagoreans and some Stoic philosophers did adopt this drastic position.

With circular time, you can be assured that after your death you will be reborn. The future will become the past. If time is like this, then the question arises as to whether there would be an endless number of times when each state of the world reoccurred, or whether, accepting Leibniz’s Principle of the Identity of Indiscernibles, each supposedly repeating state of the world would occur just once because each state would be not be discernible from the repeated state.

Islamic and Christian theologians adopted the idea that time is linear plus the Jewish-Zoroastrian idea that the universe was created at a definite moment in the past. Augustine emphasized that human experience is a one-way journey from Genesis to Judgment, regardless of any recurring patterns or cycles in nature. In the Medieval period, Thomas Aquinas agreed. Nevertheless, it was not until 1602 that the concept of linear time was more clearly formulated–by the English philosopher Francis Bacon. In 1687, Newton advocated linear time when he represented time mathematically by using a continuous straight line. The concept of linear time was promoted by Barrow, Leibniz, Locke and Kant. In 19th century Europe, the idea of linear time became dominant in both science and philosophy. However, in the twentieth century, Gödel and others discovered solutions to the equations of Einstein’s general theory of relativity that allowed closed loops of proper time. These causal loops or closed curves in spacetime allow you to go forward continuously in time until you arrive back into your past. You will become your younger self in the future. Gödel believed that even though our universe does not exemplify this solution to Einstein’s equations, the very possibility shows that time is unreal because, he believed, the concept of time does not allow loops. It is an open question in the analysis of the concept of time as to whether the concept does or does not allow loops.

e. Does Time Emerge from Something More Basic?

Is time ontologically basic, or does it depend on something more basic? We might rephrase this question as whether facts about time supervene on more basic facts. Facts about sound supervene on, or are a product of, facts about changes in the molecules of the air, so molecular change is more basic than sound. Thanks to Minkowski in 1908 we believe spacetime is more basic than time, but is spacetime itself basic? Some physicists argue that both space and time are the product of some more basic micro-substrate, although there is no agreed-upon theory of what the substrate is. Other physicists say space is not basic, but time is. In 2004, after winning the Nobel Prize in physics, David Gross expressed this viewpoint:

Everyone in string theory is convinced…that spacetime is doomed. But we don’t know what it’s replaced by. We have an enormous amount of evidence that space is doomed. We even have examples, mathematically well-defined examples, where space is an emergent concept…. But in my opinion the tough problem that has not yet been faced up to at all is, “How do we imagine a dynamical theory of physics in which time is emergent?” …All the examples we have do not have an emergent time. They have emergent space but not time. It is very hard for me to imagine a formulation of physics without time as a primary concept because physics is typically thought of as predicting the future given the past. We have unitary time evolution. How could we have a theory of physics where we start with something in which time is never mentioned?

The discussion in this section about whether time is ontologically basic has no implications for whether the word “time” is semantically basic or the concept of time is basic to concept formation.

4. What does Science Require of Time?

a. Relativity and Quantum Mechanics

The general theory of relativity and quantum mechanics are the two most fundamental theories of physics, and the Big Bang theory is the leading theory of cosmology. According to relativity and quantum mechanics, spacetime is, loosely speaking, a collection of points called “spacetime locations” where the universe’s physical events occur. Spacetime is four-dimensional and a continuum, and time is a distinguished, one-dimensional sub-space of this continuum. Any interval of time–any duration–is a linear continuum of instants. So, a duration has a point-like structure similar to the structure of an interval of real numbers; between any two instants there is another instant, and there are no gaps in the sequence of instants. This is what science requires time to be, but we haven’t commented on why science requires time to be this way.

This first response to the question “What does science require of time?” is too simple. There are complications. There is an important difference between the universe’s cosmic time and a clock’s proper time; and there is an important difference between proper time and a reference frame’s coordinate time. Most spacetimes can not have coordinate systems. Also, all physicists believe that relativity and quantum mechanics are logically inconsistent and need to be replaced by a theory of quantum gravity. A theory of quantum gravity is likely to have radical implications for our understanding of time, such as time and space being discrete rather than continuous.

Aristotle, Leibniz, Newton, and everyone else before Einstein, believed there was a frame-independent duration between two events. For example, if the time interval between two lightning flashes is 100 seconds on someone’s accurate clock, then the interval also is 100 seconds on your own accurate clock, even if you are flying by at an incredible speed. Einstein rejected this piece of common sense in his 1905 special theory of relativity when he declared that the time interval between two events is relative to (that is, depends on) the observer’s reference frame. As Einstein expressed it, “Every reference-body has its own particular time; unless we are told the reference-body to which the statement of time refers, there is no meaning in a statement of the time of an event.” Each reference frame, or reference-body, divides spacetime differently into its time part and its space part.

In 1908, the mathematician Hermann Minkowski had an original idea in metaphysics regarding space and time. He was the first person to realize that spacetime is more fundamental than either time or space alone. As he put it, “Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.” The metaphysical assumption behind Minkowski’s remark is that what is “independently real” is what does not vary from one reference frame to another. What does not vary is their union, what we now call “spacetime.” It seems to follow that the division of events into the past ones, the present ones, and the future ones is also not “independently real.” One philosophical implication is that it’s an error to say, “Only my present is real.” However, space and time are not completely equivalent even in relativity theory because time is a “distinguished” sub-space of the 4-d spacetime continuum. Being distinguished implies that time is a special dimension unlike the space dimensions, even when we confine our attention to a single reference frame. For example, a person can move easily forward and backward in any spatial dimension, but not in the time dimension.

A coordinate system or reference frame is a way of representing space and time using numbers to represent spacetime points. Science confidently assigns numbers to times because, in any reference frame, the happens-before order-relation on events is faithfully reflected in the less-than order-relation on the time numbers (dates) that we assign to events. In the fundamental theories such as relativity and quantum mechanics, the values of the time variable t in any reference frame are real numbers, not merely rational numbers. Each number designates an instant of time, and time is a linear continuum of these instants ordered by the happens-before relation, similar to the mathematician’s line segment that is ordered by the less-than relation. Therefore, if these fundamental theories are correct, then physical time is one-dimensional rather than two-dimensional, and continuous rather than discrete. These features do not require time to be linear, however, because a segment of a circle is also a linear continuum, but there is no evidence for circular time, that is, for causal loops. Causal loops are worldlines that are closed curves in spacetime.

What about instants? In mathematical physics, a duration is an ordered set of instants, not a sum of instants, just as a mathematical line is an ordered set of points, not a sum of points. That is, instants are members of durations, not parts of them. Any duration is infinitely divisible, and it endlessly divides into more intervals; it never divides into instants. The parts of durations are just more durations. Instants are like real numbers in that they are boundaries of durations. They are locations in time, but they are “in” time as members are in sets, not as parts are in wholes.

The ordering of instants by the happens-before relation, that is, by temporal precedence, is complete; there are no gaps in the sequence of instants. Knowing that an object is infinitely divisible does not tell you how many elements or ultimate parts it has, other than that there are infinitely many. It might have aleph zero or aleph one elements. No physical object is infinitely divisible; and the reason is that it can be divided into only a finite number of quarks and electrons and other particles. However, it is often convenient for certain mathematical operations to treat physical objects as if they were infinitely divisible. Physical space and physical time are generally believed to be infinitely divisible. Regarding the number of instants in any (non-zero) duration, time’s being a linear continuum implies the ordered instants are so densely packed that between any two there is a third, so that no instant has a next instant. In fact, time’s being a linear continuum implies that there is a nondenumerable infinity of instants between any two instants, that is, an aleph one number of instants. There is little doubt that the actual temporal structure of events can be embedded in the real numbers, but how about the converse? That is, to what extent is it known that the real numbers can be adequately embedded into the structure of the instants? The problem here is that, although time is not quantized in quantum theory, for times shorter than about 10-43 seconds (the so-called Planck time), science has no experimental grounds for the claim that between any two events there is a third. Instead, the justification of saying the reals can be embedded into an interval of instants is that the assumption of continuity is convenient and useful, and that there are no better theories available.

Because of quantum mechanical considerations, physicists agree that the general theory of relativity must fail for durations shorter than the Planck time, but they do not know just how it fails. Most importantly here, there is no agreement among physicists as to whether the continuum feature of time will be adopted in the future theory of quantum gravity that will be created to take account of both gravitational and quantum phenomena. The string theory of quantum gravity predicts that time is continuous, but an alternative to string theory, loop quantum gravity, does not. (See “Atoms of time.”)

Relativity theory challenges a great many of our intuitive beliefs about time. The theory is inconsistent with the common sense belief that the temporal order in which two events occur is independent of the observer’s point of reference. For events occurring at the same place, relativity theory implies the order is absolute (independent of the frame) and so agrees with common sense, but for distant events occurring close enough in time to be in each other’s absolute elsewhere, event A can occur before event B in one reference frame, but after B in another frame, and simultaneously with B in yet another frame.

Science impacts our understanding of time in other fundamental ways. Relativity theory implies there is time dilation between one frame and another. For example, the faster a clock moves, the slower it runs, relative to stationary clocks. Time dilation shows itself when a speeding twin returns to find that his (or her) Earth-bound twin has aged more rapidly. This surprising dilation result has caused some philosophers to question the consistency of relativity theory by arguing that, if motion is relative, then we could call the speeding twin “stationary” and it would follow that this twin is now the one who ages more rapidly. This argument is called the twins paradox of special relativity. Experts now are agreed that the mistake is within the argument for the paradox, not within relativity theory. The twins feel different accelerations, so their motion is not completely symmetric. As is shown in more detail in the Supplement of Frequently Asked Questions, the argument fails to notice the radically different relationships that each twin has to the rest of the universe as a whole. This is why one twin’s proper time is different than the other’s.

[An object's proper time along its worldline, that is, along its path in 4-d spacetime, is the time elapsed by a clock having the same worldline. Coordinate time is the time measured by a clock at rest in the (inertial) frame. A clock isn't really measuring the time in a reference frame other than one fixed to the clock. In other words, a clock primarily measures the elapsed proper time between events that occur along its own worldline. Technically, a clock is a device that measures the spacetime interval along its own worldline. If the clock is at rest in an inertial frame, then it measures the "coordinate time." If the spacetime has no inertial frame then it can't have a coordinate time.]

There are two kinds of time dilation. Special relativity’s time dilation involves speed; general relativity’s also involves acceleration and gravitational fields. Two ideally synchronized clocks need not stay in synchrony if they undergo different accelerations or different gravitational forces. This gravitational time dilation would be especially apparent if one of the two clocks were to fall into a black hole. A black hole can form when a star exhausts its nuclear fuel and contracts so compactly that the gravitational force prevents anything from escaping the hole, even light itself. The envelope of no return surrounding the black hole is its event horizon. As a clock falls toward a black hole, time slows on approach to the event horizon, and it completely stops at the horizon (not just at the center of the hole)–relative to time on a clock that remains safely back on Earth. Every black hole brings an end to time inside itself. If, as many physicists suspect, the microstructure of spacetime (near the Planck length which is much smaller than the diameter of a proton) is a quantum foam of changing curvature of spacetime with black holes forming and dissolving, then time loses its meaning at this small scale. The philosophical implication is that time exists only when we are speaking of regions large compared to the Planck length.

General Relativity theory may have even more profound implications for time. In 1948, the logician Kurt Gödel discovered radical solutions to Einstein’s equations, solutions in which there are closed timelike curves, so that as one progresses forward in time along one of these curves one arrives back at one’s starting point. Gödel drew the conclusion that if matter is distributed so that there is Gödelian spacetime (that is, with a preponderance of galaxies rotating in one direction rather than another), then the universe has no linear time.

b. The Big Bang

The Big Bang is a violent explosion of spacetime that began billions of years ago. It is not an explosion in spacetime. The Big Bang theory in some form or other is accepted by the vast majority of astronomers, but it is not as firmly accepted as is the theory of relativity. Here is a quick story of its origin. In 1922, the Russian physicist Alexander Friedmann predicted from general relativity that the universe should be expanding. In 1927, the Belgian physicist Georges Lemaitre suggested that galaxy movement could best be accounted for by this expansion. And in 1929, the American astronomer Edwin Hubble made careful observations of clusters of galaxies and confirmed that they are undergoing a universal expansion, on average.

Atoms are not expanding; our solar system is not expanding; even the cluster of galaxies to which the Milky Way belongs is not expanding. But most every galaxy cluster is moving away from the others. It is as if the clusters are exploding away from each other, and in the future they will be very much farther away from each other. Now, consider the past instead of the future. At any earlier moment the universe was more compact. Projecting to earlier and earlier times, and assuming that gravitation is the main force at work, the astronomers now conclude that 13.7 billion years ago the universe was in a state of nearly zero size and infinite density. Because all substances cool when they expand, physicists believe the universe itself must have been cooling down over the last 13.7 billion years, and so it begin expanding when it was extremely hot. Presently the average temperature of space in all very large regions is 2.7 degrees Celsius above absolute zero. The Big Bang theory is a theory of how our universe evolved, how it expanded and cooled from this beginning. This beginning process is called the “Big Bang.”

As far as we knew back in the 20th century, the entire universe was created in the Big Bang, and time itself came into existence “at that time.” So, asking what happened before the Big Bang was properly taken to be like asking what on Earth is north of the North Pole. With the appearance of the new theories of quantum gravity and the cosmic landscape in the 21st century, the question has been resurrected as legitimate.

In the literature in both physics and philosophy, descriptions of the Big Bang often assume that a first event is also a first instant of time and that spacetime did not exist outside the Big Bang. This intimate linking of a first event with a first time is a philosophical move, not something demanded by the science. It is not even clear that it is correct to call the Big Bang an event. The Big Bang “event” is a singularity without space coordinates, but events normally must have space coordinates. One response to this problem is to alter the definition of “event” to allow the Big Bang to be an event. Another response, from James Hartle and Stephen Hawking, is to consider the past cosmic time-interval to be open rather than closed at t = 0. Looking back to the Big Bang is then like following the positive real numbers back to ever smaller positive numbers without ever reaching a smallest positive one. If Hartle and Hawking are correct that time is actually like this, then the universe had no beginning event. But in order to simplify the discussion ahead, this article will speak of “the” Big Bang event as if it were a single origin event.

There are serious difficulties in defending the Big Bang theory’s implications about the universe’s beginning and its future. Classical Big Bang theory is based on the assumption that the universal expansion of clusters of galaxies can be projected all the way back. Yet physicists agree that the projection must fail in the Planck era, that is, for all times less than 10-43 seconds after “the” Big Bang event. Therefore, current science cannot speak with confidence about the nature of time within the Planck era. If a theory of quantum gravity does get confirmed, it should provide information about this Planck era, and it may even allow physicists to answer the question, “What caused the Big Bang?”

The scientifically radical, but theologically popular, answer, “God caused the Big Bang, but He, himself, does not exist in time” is a cryptic answer because it is not based on a well-justified and detailed theory of who God is, how He caused the Big Bang, and how He can exist but not be in time. It is also difficult to understand St. Augustine’s remark that “time itself was made by God.” On the other hand, for a person of faith, belief in their God is usually stronger than belief in any scientific hypothesis, or in any epistemological desire for a scientific justification of their remark about God, or in the importance of satisfying any philosopher’s demand for clarification.

Some physicists are advocating revision of the classical Big Bang theory in order to allow for the “cosmic landscape” or “multiverse,” in which there are multiple Big Bangs in parallel universes and an infinite amount of time before our Big Bang. See (Veneziano, 2006). In some of these universes there is no time dimension. However, this new theory is not generally accepted by theoretical cosmologists.

c. Infinite Time

There are three ways to interpret the question of whether physical time is infinite: (a) Was there an infinite amount of time in the universe’s past? (b) Is time infinitely divisible? (c) Will there be an infinite amount of time in the future?

(a) Was there an infinite amount of time in the past? Aristotle argued “yes,” but by invoking the radical notion that God is “outside of time,” St. Augustine declared, “Time itself being part of God’s creation, there was simply no before!” (that is, no time before God created everything else but Himself). So, for theological reasons, Augustine declared time had a finite past. After advances in astronomy in the late 19th and early 20th centuries, the question of the age of the universe became a scientific question. With the acceptance of the classical Big Bang theory, the amount of past time was judged to be less than 14 billion years because this is when the Big Bang began. The assumption is that time does not exist independently of the spacetime relations exhibited by physical events. Recently, however, the classical Big Bang theory has been challenged. There could be an infinite amount of time in the past according to some proposed, but as yet untested, theories of quantum gravity based on the assumptions that general relativity theory fails to hold for infinitesimal volumes. These theories imply that the beginning of the Big Bang was actually an expansion from a pre-existing physical state. There was never a singularity. In that case our Big Bang could be just one bang among other bangs throughout an infinite past of the landscape. For a discussion of these controversial theories requiring an infinite past time, see (Veneziano, 2006).

(b) Is time infinitely divisible? Yes, because general relativity and quantum mechanics require time to be a continuum. But the answer is no if these theories are eventually replaced by a relativistic quantum mechanics that quantizes time. “Although there have been suggestions that spacetime may have a discrete structure,” Stephen Hawking said in 1996, “I see no reason to abandon the continuum theories that have been so successful.”

(c) Will there be an infinite amount of time in the future? Probably. According to the classical theory of the Big Bang, the answer depends on whether events will keep occurring. The best estimate from the cosmologists these days is that the expansion of the universe is accelerating and will continue forever. There always will be the events of galaxy clusters getting farther apart, and so future time will have an infinite duration, even though gravity will continue to compact much of the matter into black holes.

There have been interesting speculations on how conscious life could continue forever, despite the fact that the available energy for life will decrease as the universe expands, and despite the fact that any life swept up into a black hole will reach the center of the hole in a finite time at which point death will be certain. For an introduction to these speculations, see (Krauss and Starkman, 2002).

d. Atoms of Time

In the classical theories of relativity and quantum mechanics, time is not quantized, but is a continuum having the character described above. However, if certain, as yet untested, theories attempting to unify relativity and quantum mechanics are correct–such as the theory of loop quantum gravity–then time is composed of discrete durations lasting about 10-43 second. There is a shortest duration for any possible event, and time is digital rather than analog.

5. What Kinds of Time Travel are Possible?

Most philosophers believe time travel is possible. In time travel, the traveler’s journey, as judged by the traveler, takes a different amount of time than the journey does as judged by those who do not take the journey. That is, there is a difference, and not merely a verbal disagreement, between the traveler’s inner time or proper time and the external or coordinate time of those who do not take the journey. However, our current scientific theories do not allow the external time lapse to be zero; so there is no “poofing” into the past or “poofing” into the future as in many science fiction stories.

According to relativity theory, there are two ways to travel into another person’s future: by moving at high speed or by taking advantage of an intense gravitational field. If you have a fast enough spaceship, you can travel to the year 4,500 C.E. on Earth. You can affect that future, not just view it. But you can not get back to your own earlier time by reversing your velocity or reversing the gravitational field. Also, your travel is to someone else’s future, not your own. You are always in your own present in this sort of relativistic time travel.

But relativity theory also allows a much stranger kind of time travel, travel to your own past. For example, in 1949 Kurt Gödel discovered a solution to Einstein’s field equations that allows continuous, closed future-directed timelike curves. To say this more simply, Gödel discovered that in some possible worlds that obey the theory of general relativity, you can eventually arrive into your own past. In this unusual non-Minkowski spacetime, the universe as a whole is the time machine; no one needs to build a machine to travel this way. Relativity theory even permits you to travel back and meet yourself as a child. But, although you can meet yourself, you can not change what has happened in the past. You can’t go back and prevent Adolf Hitler from gaining political power in Germany in the 1930s. Despite time travel to the past being apparently consistent with Einstein’s general theory of relativity, there are several well known arguments against the physical possibility of travel to the past. Despite the controversy, none are generally considered to be decisive.

1.If you encountered someone who claimed to be a time traveler, what could you do to verify the claim? There’s nothing you could do, therefore there will never be a good reason to believe in time travel.
2.Time travel is impossible because if it were possible we should have seen many time travelers by now, but nobody has encountered any time travelers.
3.And time travel is impossible because, if there were time travel, then when time travelers go back and attempt to change history they must always botch their attempts to change anything, and it will appear to anyone watching them at the time as if nature is conspiring against them. Since observers have never witnessed this apparent conspiracy of nature, there is no time travel.
4.If there were travel to the past along a closed timelike curve, then these events would occur before themselves and after themselves, but this violates our definition of word “before,” or violates our concept of time, so this odd solution of Einstein’s equations is not a physically realistic solution.
5.Travel to the past is impossible because it allows the gaining of information for free. For example, print out this article that you are reading. Enter a time machine with it. Give me the article before I ever thought about time travel. I then publish it as this article in this encyclopedia. This all seems to be consistent with relativity theory, but who first came up with the information in this article? You had it before I did, but you obtained it from me.
6.Probing the possibility of a contradiction in backwards time travel, the American philosopher John Earman has described a rocket ship that carries a very special time machine. The time machine is capable of firing a probe into its own past. Suppose the ship is programmed to fire the probe on a certain date unless a safety switch is on. Suppose the safety switch is programmed to be turned on if and only if the “return” or “impending arrival” of the probe is (or has been) detected by a sensing device on the ship. Does the probe get launched? It is launched if and only if it is not launched. The way out of Earman’s paradox seems to require us to accept that (a) the universe conspires to keep people from building the probe or the safety switch or an effective sensing device, or (b) time travel probes must go so far back in time that they never survive and make it back to the time when they were launched, or (c) time travel into the past is impossible.
For more discussion of time travel, see the encyclopedia article “Time Travel.”

6. Is the Relational Theory Preferable to the Absolute Theory?

Absolute theories are theories that imply time exists independently of the spacetime relations exhibited by physical events. Relational theories imply it does not. Some absolute theories describe spacetime as being like a container for events. The container exists with or without events in it. Relational theories imply there is no container without contents. John Norton’s metaphors might help. Our universe is like a painting, and absolute spacetime is like the painter’s canvas. If you take away the paint (the spacetime events) from the painting, you still have the canvas. Relational spacetime is like citizenship. Take away the citizens (the spacetime events), and you have no citizenship left.

Everyone agrees time cannot be measured without there being objects and changes, but the present issue is whether it exists without objects and changes. The absolute or substantival theories are theories that spacetime could exist even if there were no physical objects and events in the universe, but relational theories imply that spacetime is nothing but objects, their events, and the spatiotemporal relationships among objects and their events, so that spacetime reduces to sets of possible spatiotemporal relations.

There are two senses of “absolute” that need to be distinguished. As we are using the term, it means independent of the events. A second sense of “absolute” means independent of observer or reference frame. Einstein’s theory implies there is no absolute time in this second sense. Aristotle accepted absolute time in this second sense, but he rejected it in our sense of being independent of events and took the relationalist position that, “neither does time exist without change.” [Physics, 218b]

However, the battle lines were most clearly drawn in the early 18th century when Leibniz argued for the relationalist position against Newton, who had adopted an absolute theory of time. Leibniz’s principal argument against Newton is a reductio ad absurdum. Suppose Newton’s absolute space and time were to exist. But one could then imagine a universe just like ours except with everything shifted five miles east and five minutes earlier. However, there would be no reason why this shifted universe does not exist and ours does. Now we have arrived at a contradiction because, if there is no reason for our universe over the shifted universe, then we have violated Leibniz’s Principle of Sufficient Reason: that there is an understandable reason for everything being the way it is. So, Newton’s absolute space and time do not exist. In short, the trouble with Newton’s absolutism is that it leads to too many unnecessary possibilities.

Newton offered this two-part response: (1) Leibniz is correct to accept the Principle of Sufficient Reason regarding the rational intelligibility of the universe. But there do not have to be knowable reasons for humans; God might have had His own sufficient reason for creating the universe at a given place and time even though mere mortals cannot comprehend His reasons. (2) The bucket thought-experiment shows that acceleration relative to absolute space is detectable; thus absolute space is real, and if absolute space is real, so is absolute time. Suppose we tie a bucket’s handle to a rope hanging down from a tree branch. Partially fill the bucket with water, and let it come to equilibrium. Notice that there is no relative motion between the bucket and the water, and in this case the water surface is flat. Now spin the bucket, and keep doing this until the angular velocity of the water and the bucket are the same. In this second case there is also no relative motion between the bucket and the water, but now the water surface is concave. So spinning makes a difference, but how can a relational theory explain the difference in the shape of the surface? It can not, says Newton. When the bucket and water are spinning, what are they spinning relative to? Because we can disregard the rest of the environment including the tree and rope, says Newton, the only explanation of the difference in surface shape between the non-spinning case and the spinning case is that when it is not spinning there is no motion relative to absolute space, but when it is spinning there is motion relative to space itself, and thus space itself is acting upon the water surface to make it concave. Alternatively expressed, the key idea is that the presence of centrifugal force is a sign of rotation relative to absolute space. Leibniz had no rebuttal. So, for many years thereafter, Newton’s absolute theory of space and time was generally accepted by European scientists and philosophers.

One hundred years later, Kant entered the arena on the side of Newton. In a space containing only a single glove, said Kant, Leibniz could not account for its being a right glove versus a left glove because all the internal relationships would be the same in either case. However, we all know that there is a real difference between a right and a left glove, so this difference can only be due to the glove’s relationship to space itself. But if there is a “space itself,” then the absolute theory is better than the relational theory.

Newton’s absolute theory of time was dominant in the 18th and 19th centuries, even though during those centuries Huygens, Berkeley, and Mach had entered the arena on the side of Leibniz. In the 20th century, Reichenbach and the early Einstein declared the special theory of relativity to be a victory for the relational theory. Special relativity, they said, ruled out a space-filling aether, the leading candidate for absolute space, so the absolute theory was incorrect. And the response to Newton’s bucket argument is to note Newton’s error in not considering the environment. Einstein agreed with Mach’s view of the 19th century that, if you hold the bucket still but spin the background stars, the water will creep up the side of the bucket. Although it was initially thought by Einstein and others that relativity theory supported Mach, Lawrence Sklar (Sklar, 1976, pp. 219-21) argues that this may not be correct.

Many philosophers argue that Reichenbach and the early Einstein have been overstating the amount of metaphysics that can be extracted from the physics. Remember the ambiguity in “absolute” mentioned above? There is absolute in the sense of independent of reference frame and absolute in the sense of independent of events. Which sense is ruled out when we reject a space-filling aether? The critics admit that general relativity does show that the curvature of spacetime is affected by the distribution of matter, so today it is no longer plausible for an absolutist to assert that the “container” is independent of the matter it contains. But, so they argue, general relativity does not rule out a more sophisticated absolute theory–to be discussed below. By the end of the 20th century, absolute theories had gained some ground thanks to the arguments of John Earman, Michael Friedman, Adolf Grünbaum, and Tim Maudlin.

In 1969, Sydney Shoemaker presented an argument to convince us of the understandability of time existing without change, as Newton’s absolutism requires. Divide space into three disjoint regions, called region 3, region 4, and region 5. In region 3, change ceases every third year for one year. People in regions 4 and 5 can verify this and convince the people in region 3 after they come back to life at the end of their frozen year. Similarly, change ceases in region 4 every fourth year for a year; and change ceases in region 5 every fifth year. Every sixty years, that is, every 3 x 4 x 5 years, all three regions freeze simultaneously for a year. In year sixty-one, everyone comes back to life, time having marched on for a year with no change. But philosophers of time point out that, even if Shoemaker’s scenario shows time’s existing without change is understandable, the deeper question is whether time does exist without change.

Here is one argument that it does. Must the relationist say there can be no “empty” time? If events occur in a room before and after 11:01 AM, but not exactly at 11:01 AM, must the relationalist say there never was a time of 11:01 AM in the room? To avoid saying “yes,” which would be absurd, a relationalist might say 11:01 exists in the room and everywhere else because somewhere outside the room something is happening then, and somehow or other sense can be made of time in the room in terms of these external events. The absolutist then asks us to consider the possibility that the room is the whole universe. In that case, the relationalist response to losing 11:01 AM would probably be to say possible events occur then in the room even if actual events do not. But now look where we are, says the absolutist. If the relational theory is going to consider spacetime points to be permanent possibilities of the location of events, then the relationalist theory collapses into substantivalism. This is because, to a substantivalist, a spacetime point is also just a place where something could happen.

Hartry Field offers another argument for the absolute theory by pointing out that modern physics requires gravitational and electromagnetic fields that cover spacetime–a light wave, say, is considered to be a ripple in the field. The fields are states of spacetime, with the field having a value (a number or vector) at points throughout the field. These fields cannot be states of some Newtonian aether, but there must be something to have the field properties. What else except substantive spacetime points?

7. Does Time Flow?

“It is as if we were floating on a river, carried by the current past the manifold of events which is spread out timelessly on the bank,” said one philosopher trying to capture time’s flow with a helpful metaphor. Santayana offered another: “The essence of nowness runs like fire along the fuse of time.” The philosopher’s goal is to clarify the idea of time’s flow, the passage of time. Everyone agrees that the passage of time “appears” to us humans to flow, although few scientists or philosophers believe that all conscious beings recognize the flow; hawks do not, although they are apt at spotting the movements of their prey. Even if time does flow, there is the additional question of whether the flow can change. Can physical time’s flow be slower on Friday afternoon, compared to Monday morning?

There are two categories of theories of time’s flow. The first, and most popular among physicists, is that the flow is an illusion, the product of a faulty metaphor. Time exists, things change, but time does not flow objectively, although there may well be some objective feature of our brains that causes us to believe we are experiencing a flow of time; but in that case time flows only in a subjective sense of the term. The theory is sometimes characterized as a “myth-of-passage” theory. As we shall see, this theory of time’s flow is normally the one adopted by those who believe McTaggart’s B-series is more fundamental than his A-series.

The second category of theories of time’s flow contains theories implying that the flow is objective, a feature of our mind-independent reality that is to be found in, say, today scientific laws, or, if it has been missed there, then in future scientific laws. These theories are called “dynamic theories” of time. This sort of theory of time’s flow is closer to common sense, and has historically been the more popular theory among philosophers.

Some dynamic theories imply that the flow is a matter of events changing from being indeterminate in the future to being determinate in the present and past. Time’s flow is really events becoming determinate. Thus dynamic theorists speak of time’s flow as “temporal becoming.” Another dynamic theory implies that the flow is a matter of events changing from being future, to being present, to being past. This is the kind of flow associated with McTaggart’s A-series of events.

Opponents of dynamic theories complain that when events change in these senses, the change is not a real change in the event’s essential, intrinsic properties, but only in the event’s relationship to the observer. For example, saying the death of Queen Anne is an event that changes from present to past is no more of a real change in the event than saying her death changed from being approved of to being disapproved of. This extrinsic change in approval does not count as a real change in her death, and neither does the so-called change from present to past. Attacking the notion of time’s flow in this manner, Grünbaum said: “Events simply are or occur…but they do not ‘advance’ into a pre-existing frame called ‘time.’ …Time is a system of relations between events, and as events are, so are their relations. An event does not move and neither do any of its relations.” So, Grünbaum denies the objective nature of McTaggart’s A-series and points out that the flow of time is an illusion or myth.

Instead of arguing that events change their properties, some advocates of the dynamic theory of time embrace the flow of time by saying that the flow is reflected in the change over time of truth values of a sentence or proposition. For example, the sentence “It is now raining” was true during the rain yesterday but has changed to false on today’s sunny day. It is these sorts of truth value changes that are at the root of time’s flow. In response, critics suggest that the indexical (or token reflexive) sentence “It is now raining” has no truth value because the reference of “now” is unspecified. If it can not have a truth value, it can not change its truth value. However, the sentence is related to a sentence that does have a truth value. Supposing it is now midnight here on April 1, 2007 in Sacramento, California, then the indexical sentence “It is now raining” is related to the complete or context-explicit sentence “It is raining at midnight on April 1, 2007 in Sacramento.” Only these non-indexical, non-context-dependent, complete sentences have truth values, and these truth values do not change with time. So, events do not change their properties because complete sentences do not change their truth values.

Other advocates of the dynamic theory of time ask us to analyze time’s flow in terms of facts that come into existence. This coming into existence of facts, the actualization of new states of affairs, is time’s flow.

Tim Maudlin argues for a version of the dynamic theory that is very different than all of the above. He argues that the objective flow of time is fundamental and unanalyzable; it is a fundamental, irreducible fact that time passes, and this passage just is the flow of time. He is happy to say “time does indeed pass at the rate of one hour per hour” (Maudlin, 2007, p. 112), although other philosophers have called this rate “meaningless.” Maudlin also is an advocate of the block universe theory and believes the passage of time is an ingredient of this single block entity.

Regardless of how the metaphor of time’s flow is analyzed, or even if it is taken as fundamentally unanalyzable, the passage of time implies a direction of time.

8. What Gives Time its Direction or “Arrow”?

a. What Needs to be Explained

The arrow of time is what distinguishes a group of events ordered by the happens-before relation from those ordered by its converse, the happens-after relation. Time’s arrow is evident in the process of mixing cool cream into hot coffee. You soon get lukewarm coffee, but you never notice the reverse–lukewarm coffee separating into a cool part and a hot part. Such is the way this irreversible thermodynamic process goes. Time’s arrow is also evident when you prick a balloon. The air inside the balloon rushes out; it never stays in the balloon as it was before the pricking. So, the pricking starts an irreversible process. The arrow of a physical process is the way it normally goes, the way it normally unfolds through time. If a process goes only one-way, we call it an “irreversible process.” (Strictly speaking, a reversible process is one that is reversed by an infinitesimal change of its surrounding conditions, but we can overlook this fine point because of the general level of the present discussion.) The amalgamation of the universe’s irreversible processes produces the cosmic arrow of time, the master arrow. Usually this arrow is what is meant when one speaks simply of “time’s arrow.” By convention, we say the arrow is directed toward the future.

There are many goals for a fully developed theory of time’s arrow. It should tell us (1) why this arrow exists; (2) why the arrow is apparent in macro processes but not micro processes; (3) what it would be like for the arrow to reverse direction; (4) what the relationships are among the various more specific arrows of time–the various temporally asymmetric processes such as entropy increases [the thermodynamic arrow], causes preceding their effects [the causal arrow], light radiating from its source rather than converging into it [the electromagnetic arrow], and our knowing the past more easily than the future [the knowledge arrow]; and (5) what are the characteristics of a physical theory that pick out a preferred direction in time.

Because the physical processes we commonly observe do have an arrow, you might think that an inspection of the basic physical laws would readily reveal time’s arrow. It will not. With very minor exceptions, all the basic laws of fundamental processes are time symmetric. (It is assumed here that the second law of thermodynamics is not basic but somehow derived.) This means, according to a principal definition of time symmetry, that if a certain process is allowed by the laws, then that process reversed in time is also allowed, and either direction is as probable as the other. Maxwell’s equations of electromagnetism, for example, can be used to predict that television signals can exist, but the equations do not tell us whether those signals arrive before or arrive after they are transmitted. In other words, these basic laws of science do not imply an arrow of time.

Suppose you have a movie of a basic physical process such as two electrons bouncing off each other. You can not actually create this movie because the phenomenon is too small, but forget that fine point for a moment. If you had such a movie, you could run it forwards or backwards, and both showings would illustrate a possible process according to the basic laws of science, and they would be equally probable processes. You could not tell from just looking at the movie whether you were looking at the original or at it being shown backwards in time. So, time’s arrow is not revealed in this microscopic process.

The “disappearance” of time’s arrow in microscopic process, does not show that time itself fades away as you look at briefer and smaller processes; this is because there are still events happening, and so time still exists there. Also, it is important to note that, although it is interesting to explain how we humans are able to detect the arrow, the more challenging philosophical question is to explain why time has an arrow.

b. Explanations or Theories of the Arrow

In the 19th century, the new kinetic theory of gases was supposed to provide the foundation for all gas behavior, yet this foundational theory is time symmetric. That is, the theory is insensitive to the arrow of time, to the distinction between past and future–because a moving molecule could just as well move in one direction as in the reverse direction. How were the physicists to resolve this apparent contradiction of having a temporally symmetric theory at the foundation of a theory that is supposed to account for irreversible gas processes such as the escape of gas from a balloon pricked with a pin? The first clue was discovered in the mid-19th century by the German physicist Rudolf Clausius. He devised an early version of the 2nd law of thermodynamics, which, speaking informally, is the claim that a isolated system will evolve to be more disordered or complex, with some of its useful energy converting to heat. [A isolated system is a system left to itself; it is a region isolated from outside influences, a region where energy can not come in or go out.] That is,

(a) 2nd Law: In an isolated system, entropy never decreases.

Entropy is Clausius’s word for the measure of this disorder; it measures the conversion of useful to “useless” energy by irreversible processes. As R. A. Fisher expressed it, entropy changes lead to a progressive disorganization of the physical world, at least from the human standpoint of the utilization of energy. As time goes on, some sub-systems do become progressively more organized, such as when we build a house on a bare lot, but this organization is at the expense of a greater degree of disorganization elsewhere such as the depletion of natural resources and the digestion of food by the house builders and, ultimately, the degradation of the sun.

It seemed to many physicists, beginning with Ernst Mach, that time’s arrow–in all processes and not just in gas behavior–is reducible to or grounded in entropy increase. This implies that in a universe in maximum equilibrium where entropy changes are absent, there will not be an arrow of time. This entropy theory of time’s arrow implies that our having traces of the past but not of the future reduces to entropy increases, as does our inclination to say causes happen before their effects rather than after.

Another deep question is, “Why should there be more disorder in the future?” The Austrian physicist Ludwig Boltzmann had an answer in 1872. Boltzmann claimed that it is a matter of probability because, for complex systems, that is, systems with many particles, disordered states of the system are more probable than ordered states. There are many more microstates in which, from a macro perspective, the system is disordered than microstates in which the system is ordered, so it is very probable that the system will naturally end up in the most generic possible macrostate. Boltzmann redefined the concept of entropy in terms of the statistics of molecular motion, and he deduced a revised 2nd law from probability theory:

(b) 2nd Law: In an isolated system, entropy is likely not to decrease.

His treatment of entropy as being basically a statistical concept was broadly accepted, as was Mach’s and his claim that time’s arrow is to be explained in terms of entropy increase.

Boltzmann’s achievement soon had to confront two obstacles, one from Henri Poincaré and one from Josef Loschmidt. First, Poincaré. A dynamic system is a system defined by the values of the positions and velocities of all the system’s particles–such as the places and speeds of the molecules in a cup of coffee. Poincaré’s recurrence theorem in statistical mechanics says every isolated dynamical system will eventually return to a state as close to the initial state as we might wish. Wait long enough, and the lukewarm coffee will separate into hot coffee and cool cream. This reversal would be expected to take 10N seconds, where N is the number of molecules involved. The number is staggering, but still finite; so, strictly speaking, there are no irreversible processes and no long term entropy increase. Whenever entropy rises it will eventually fall. That implies there is an apparent contradiction between Poincaré’s theorem and Boltzmann’s.

To avoid this Poincaré problem, physicists redefined the second law:

(c) 2nd Law: In an isolated system, entropy is likely not to decrease for any period of time that is short compared to the Poincaré period for that system.

Josef Loschmidt pointed out another problem with Boltzmann’s approach to the arrow of time. Loschmidt realized that Boltzmann’s statistical mechanics predicts for any point in time not only that entropy should be higher in the future but also that it should be higher in the past. However, we know that it was not higher in the past. Here is a graph representing this knowledge.

The conclusion to be drawn from this is that entropy increase is only part of the story of time’s cosmic arrow.

Loschmidt suggested that the low entropy in the past must be explained by what the initial conditions happened to be like at the beginning of the universe. Boltzmann agreed. Among cosmologists, this is now the generally accepted answer to the origin of time’s arrow.

Yet this answer leads naturally to the request for an explanation of the initial configuration of our universe. Is this temporally asymmetric initial boundary condition simply a brute fact, as many physicists believe, or are there as yet undiscovered laws to explain the fact, as many other physicists believe–either to explain it as necessarily having had to happen or to explain it as having been highly probable? Objecting to inexplicable initial facts as being unacceptably ad hoc, the Swiss physicist Walther Ritz and, more recently, Roger Penrose, say we must not yet have found the true laws (or invented the best laws) underlying nature’s behavior. We need to keep looking for basic, time asymmetrical laws in order to account the initial low entropy and thus for time’s arrow.

The low entropy appears to be due to the microscopic Big Bang region having just the right amount of homogeneity or smoothness so that galaxies would eventually form. If it were initially smoother, then there would be no congealing of matter into galaxies; if it were initially less smooth, then most all the matter would have long ago ended up in large black holes. So, the issue of how to explain the thermodynamic arrow is the issue of why the Big Bang region had just the right smoothness.

c. Multiple Arrows

Consider the difference between time’s arrow and time’s arrows. The direction of entropy change is the thermodynamic arrow. Here are some suggestions for additional arrows:

a. There are records of the past but not of the future.
b. It is easier to know the past than to know the future.
c. Light and radio waves spread out from, but never converge into, a point.
d. The universe expands rather than shrinks.
e. Causes precede their effects.
f. We see black holes but never white holes.
g. Conscious actions affect the future but not the past.
h. B meson decay, neutral kaon decay, and Higgs boson decay are each different in a time reversed world.
i. Quantum mechanical measurement collapses the wave function.
j. Possibilities decrease as time goes on.

Most physicists suspect all these arrows are linked so that we can not have some arrows reversing while others do not. For example, the collapse of the wave function is generally considered to be due to an increase in the entropy of the universe. However, the linkage of all the arrows may require as yet undiscovered laws.

d. Reversing Time

But could all the arrows have pointed the other way? That is, could the cosmic arrow of time have gone the other way? Most physicists suspect that the answer is yes, and it would have gone the other way if the initial conditions of the universe at the Big Bang had been different.

Should we also expect that at some time in the future all the arrows will reverse? Unfortunately, it is still an open question in philosophy as to what it means for time’s arrow to reverse. For a technical introduction to the debate, see Savitt, pp. 12-19.

Supposing the cosmic arrow of time were to reverse, it would be possible for our past to be re-created and lived in reverse order. This re-occurrence of the past is different than the re-living of past events via time travel. With cyclical time or with time travel in a causal loop, the past is re-visited in the original order that the past events occurred; the past is not visited in reverse order.

Philosophers have gone on to ask other interesting questions about different scenarios involving the reversal of time’s arrow. Suppose the cosmic arrow of time were someday to reverse in a distant, populated region far away from Earth. Imagine what life would be like for the time-reversed people. First off, would it be possible for them to be conscious? Assuming consciousness is caused by brain processes, could there be consciousness if their nerve pulses reversed, or would this reversal destroy consciousness? This is a difficult question, but supposing the answer is that they would be conscious, and supposing that anyone’s future is what will happen, not what has happened, then what would their experience be like? It has been suggested that if we were able to watch them in their region of space, they would appear to us to be pre-cognitive. Could they use this to win gambling bets on, say, the roll of the dice? Probably not, say other philosophers who argue that the inner experience of time-reversed people must be no different than ours.

If Aristotle were correct that the future, unlike the past, is undetermined or open, then the future of people in the time-reversed region would be open, too. But it is like our past. What can we conclude from this? Do we conclude that our past might really be undetermined and open, too? That our past could change?

And there are other questions. Consider communication between the two regions. If we sent a signal to the time-reversed region, could our message cross the border, or would it dissolve there, or would it bounce back? If they successfully sent a recorded film across the border to us, should we play it in the ordinary way or in reverse? If the arrow of time were to reverse in some region, would not dead people in that region become undead, but is that metaphysically possible?

9. Is Only the Present Real?

Have past objects, such as dinosaurs, slipped out of existence? More generally, we are asking whether the past is real. How about the future? Philosophers are divided into three camps on the question of the reality of the past, present, and future. The presentist viewpoint maintains that the past and the future are not real, and that only the present is real, so if a statement about the past is true, this is because some present facts make it true. Advocates of a growing past argue that, in addition to the present, the past is also real. Reality “grows” with the coming into being of determinate reality from an indeterminate or potential reality. “The world grows by accretion of facts,” says Richard Jeffrey. Aristotle (in De Interpretatione, chapter 9) and C. D. Broad advocated a growing-past theory. Parmenides, Duns Scotus and A. N. Prior are presentists.

Opposing both presentism and the growing past theory, Bertrand Russell, J.J.C. Smart, W.V.O. Quine, Adolf Grünbaum, and Paul Horwich object to assigning special ontological status to the present. They say there is no objective ontological difference among the past, the present, and the future just as there is no ontological difference between here and there. Yes, we thank goodness that the pain is there rather than here, and past rather than present, but these differences are subjective, being dependent on our point of view. This ontology of time is called the block universe theory because it regards reality as a single block of spacetime with its time slices ordered by the temporally-before relation. It is mental perspectives only that divide the block into a past part, a present part, and a future part. The future, by the way, is the actual future, not all possible futures. William James coined the term “block universe,” but the theory is also called “eternalism” and the “static theory of time.”

Although presentists say dinosaurs are not real, whereas eternalists say that dinosaurs are as real as anything in the present, another camp of philosophers argue that the presentist-eternalist debate is merely verbal because each side is using the word “real” in a different sense; the presentist uses it in a tensed sense, whereas the eternalist uses it in an untensed sense.

The presentist and the advocate of the growing past will usually unite in opposition to the block universe (eternalism) on the grounds that it misses the special “open” character of the future and the equally significant point that the present is so much more vivid to a conscious being than is any other time-slice of spacetime. The advocates of the block universe counter that only the block universe can make sense of relativity’s implication that, if people are in certain relative motions, an event in person A’s present can be in person B’s future. Presentism and the growing-past theories must suppose that this event is both real and unreal because it is real for A but not real for B. Surely that conclusion is unacceptable, they claim. Their two key assumptions here are that relativity does provide an accurate account of the spatiotemporal relations among events, and that if there is some frame of reference in which two events are simultaneous, then if one of the events is real, so is the other.

Opponents of the block universe charge that it does not provide an accurate account of the way things are because it leaves out “the now” or “the present.” This metaphysical dispute was fueled by Einstein who said:

Since there exists in the four dimensional structure no longer any slices which represent “now” objectively…it appears more natural to think of physical reality as a four dimensional existence instead of, as hitherto, the evolution of a three dimensional existence.

Many philosophers, however, do not agree with Einstein.

This philosophical dispute has taken a linguistic turn by focusing upon a question about language: “Are predictions true or false at the time they are uttered?” Those who believe in the block universe (and thus in the determinate reality of the future) will answer “Yes” while a “No” will be given by presentists and advocates of the growing past. The issue is whether contingent sentences uttered now about future events are true or false now rather than true or false only in the future at the time the predicted event is supposed to occur.

Suppose someone says, “Tomorrow the admiral will start a sea battle.” And suppose that tomorrow the admiral orders a sneak attack on the enemy ships. And suppose that this action starts a sea battle. Advocates of the block universe argue that, if so, then the above sentence was true all along. Truth is eternal or fixed, they say, and “is true” is a tenseless predicate, not one that merely says “is true now.” These philosophers point favorably to the ancient Greek philosopher Chrysippus who was convinced that a contingent sentence about the future is true or false, and it can not be any value in between such as “indeterminate.” Many others, following a suggestion from Aristotle, argue that the sentence is not true until it can be known to be true, namely at the time at which the sea battle occurs. The sentence was not true before the battle occurred. In other words, predictions have no (classical) truth values at the time they are uttered. Predictions fall into the “truth value gap.” This position that contingent sentences have no classical truth values is called the Aristotelian position because many researchers throughout history have taken Aristotle to be holding the position in chapter 9 of On Interpretation–although today it is not so clear that Aristotle himself held it.

The principal motive for adopting the Aristotelian position arises from the belief that if sentences about future human actions are now true, then humans are fated (or determined) to perform those actions, and so humans have no free will. To defend free will, we must deny truth values to predictions.

The Aristotelian argument against predictions being true or false has been discussed as much as any in the history of philosophy, and it faces a series of challenges. First, if there really is no free will, or if free will is compatible with fatalism (or determinism), then the motivation to deny truth values to predictions is undermined.

Second, if it is true that you will perform an action in the future, it does not follow that now you will not perform it freely, nor that you are not free to do otherwise, but only that you will not do otherwise. For more on this point about modal logic, see Foreknowledge and Free Will.

A third challenge arises from moral discussions about the interests of people who are as yet unborn. Quine argues that if we have an obligation to conserve the environment for these people, then we are treating them as being as real as the people around us now. Only the block universe view can make sense of this treatment.

A fourth challenge, from Quine and others, claims the Aristotelian position wreaks havoc with the logical system we use to reason and argue with predictions. For example, here is a deductively valid argument:

There will be a sea battle tomorrow.

If there will be a sea battle tomorrow, then we should wake up the admiral.

So, we should wake up the admiral.

Without the premises in this argument having truth values, that is, being true or false, we cannot properly assess the argument using the standard of deductive validity because this standard is about the relationships among truth values of the component statements. Unfortunately, the Aristotelian position says that some of these components are neither true nor false, so Aristotle’s position is implausible.

In reaction to this fourth challenge, proponents of the Aristotelian argument claim that if Quine would embrace tensed propositions and expand his classical logic to a tense logic, he could avoid those difficulties in assessing the validity of arguments that involve sentences having future tense.

Quine has claimed that the analysts of our talk involving time should in principle be able to eliminate the temporal indexical words because their removal is needed for fixed truth and falsity of our sentences [fixed in the sense of being eternal sentences whose truth values are not relative because the indicator words have been replaced by times, places and names, and whose verbs are treated as tenseless], and having fixed truth values is crucial for the logical system used to clarify science. “To formulate logical laws in such a way as not to depend thus upon the assumption of fixed truth and falsity would be decidedly awkward and complicated, and wholly unrewarding,” says Quine.

Philosophers are still very divided on the issues of whether only the present is real, what sort of deductive logic to use, and whether future contingent sentences have truth values.

10. Are there Essentially Tensed Facts?

All the world’s cultures have a conception of time, but in only half the world’s languages is the ordering of events expressed in the form of tense (Pinker, p. 189). The English language, for example, expresses conceptions of time with tenses but also with aspect and with adverbial time phrases such as “now,” “tomorrow” and “twenty-three days ago.” Philosophers have asked what we are basically committed to when we use tenses to “locate” an event in the past, in the present, or in the future. For example, what do we make of the past tense verb in saying, “Mohammed’s birth occurred centuries ago”? There are two major answers. One answer is that tense distinctions represent objective features of reality that are not captured by the popular block universe approach. This answer takes tenses very seriously and is called the tensed theory of time, or the A-theory in McTaggart’s sense of A vs. B. A second answer to the question of the significance of tenses is that they are subjective features of the perspective from which the subject views the universe. Actually this disagreement isn’t really about tenses in the grammatical sense, but about the significance of the distinctions of past, present, and future which those tenses are used to mark.

On the tenseless theory of time, or the B-theory, whether the birth of Mohammed occurred there depends on the speaker’s perspective; similarly, whether the birth occurs then is equally subjective. The proponent of the tenseless view does not deny the importance or coherence of talk about the past, but will say it really is (or should be analyzed as being) talk about our own relation to events. My assertion that Mohammed’s birth has occurred might be analyzed as asserting that the birth event happens before the event of my writing this sentence.

This controversy is often presented as a dispute about whether tensed facts exist, with advocates of the tenseless theory objecting to tensed facts such as the fact of Mohammed’s having been born. The primary function of tensed facts is to make tensed sentences true. For the purposes of explaining that point, let us uncritically accept the Correspondence Theory of Truth and apply it to the following past tense sentence:

Custer died in Montana.

If we apply the Correspondence Theory directly to this sentence, we would say that

The sentence “Custer died in Montana” is true because it corresponds to the tensed fact that Custer died in Montana.

Opponents of tensed facts argue that the Correspondence Theory should be applied only indirectly. One approach, the classical tenseless approach, argues that the Correspondence Theory should be applied only to the result of analyzing away tensed sentences into equivalent sentences that do not use tenses. They might say that the sentence “Custer died in Montana” has this equivalent “eternal” sentence:

There is a time t such that Custer dies in Montana at time t, and time t is before the time of the writing of the sentence “Custer died in Montana” by Dowden in the article “Time” in The Internet Encyclopedia of Philosophy.

In this analysis, the verb dies is logically tenseless (although grammatically it is present tensed). Applying the Correspondence Theory to this new sentence yields:

The sentence “Custer died in Montana” is true because it corresponds to the tenseless fact that there is a time t such that Custer dies in Montana at time t, and time t is before the time of the utterance (or writing) of the sentence “Custer died in Montana” by Dowden in the article “Time” in The Internet Encyclopedia of Philosophy

This analysis of tenses without appeal to tensed facts is challenged on the grounds that it can succeed only for utterances or inscriptions, but a sentence can be true even if never uttered or written by anyone. There are other challenges. Roderick Chisholm and A. N. Prior claim that the “is” in the sentence “It is now midnight” is essentially present tensed because there is no translation using only tenseless verbs. Trying to analyze it as, say, “There is a time t such that t = midnight” is to miss the essential reference to the present in the original sentence. The latter sentence is always true, but the original is not, so the tenseless analysis fails. There is no escape by adding “and t is now” because this last indexical still needs analysis, and we are starting a vicious regress.

Chisholm and Prior say that true sentences using the temporal indexical terms “now,” “before now,” and “happened yesterday” are part of the facts of the world that science should account for, and science fails to do this because it does not recognize them as being real facts. Science, they say, so far restricts itself to eternal facts, such as in the Minkowski-like spacetime representation of events. These events are sets of spacetime points. For such events, the reference to time and place is explicit. A Minkowski spacetime diagram displays only what happens before what, but not which time is present time, or past, or future. What is missing from the diagram, say Chisholm and Prior, is some moving point on the time axis representing the observer’s “now” as time flows up the diagram.

Earlier, Prior [1959] had argued that after a painful event,

one says, e.g., “Thank goodness that’s over,” and [this]…says something which it is impossible that any use of a tenseless copula with a date should convey. It certainly doesn’t mean the same as, e.g., “Thank goodness the date of the conclusion of that thing is Friday, June 15, 1954,” even if it be said then. (Nor, for that matter, does it mean “Thank goodness the conclusion of that thing is contemporaneous with this utterance.” Why should anyone thank goodness for that?).

D. H. Mellor, who advocates a newer subjective theory of tenses, says there’s no mystery about the meaning of tensed sentences that requires tensed facts or tensed properties. More specifically, he argues that the truth conditions of any tensed sentence can be explained without tensed facts even if Chisholm and Prior are correct that some tensed sentences can not be translated into tenseless ones. Mellor would say it is not the pastness of the painful event that explains why I say, “Thank goodness that’s over.” My gladness is explained by my belief that the event is past, plus its being true that the event is past. In addition, tenseless sentences can be used to explain the logical relations between tensed sentences: that one tensed sentence implies another, is inconsistent with yet another, and so forth. And understanding truth conditions and truth implications is the main thing you know when you understand a declarative sentence. In other words, the meaning of tensed sentences can be explained without utilizing tensed properties or tensed facts. Then Ockham’s Razor is applied. If we can do without essentially tensed facts, then we should say essentially tensed facts do not exist. To summarize, tensed facts were presumed to be needed to account for the truth of tensed talk; but the analysis shows that ordinary tenseless facts are adequate. So, there are no essentially tensed facts, according to Mellor.

11. What is Temporal Logic?

Temporal logic is the representation of information about time by using the methods of symbolic logic. The classical approach to temporal logic is via tense logic, a formalism that adds tense operators to an existing system of symbolic logic. The pioneer in the late 1950s was A. N. Prior. He created a new symbolic logic to describe our use of time words such as “now,” “happens before,” “afterwards,” “always,” and “sometimes”. The relationships that propositions have to the past, present, and future help to determine their truth-value. A proposition, such as “Socrates is sitting down” is allowed to be true at one time and false at another time.

Prior was the first to appreciate that time concepts are similar in structure to modal concepts such as “it is possible that” and “it is necessary that,” and so he adapted modal propositional logic for his tense logic. Dummett and Lemmon also made major, early contributions to tense logic.

One standard system of tense logic is a variant of the S4.3 system of modal logic. In this formal tense logic, the usual modal operator “it is possible that” is re-interpreted to mean “at some past time it was the case that.” Let the letter “P” represent this operator, and add to the axioms of classical propositional logic the modal-like axiom P(p v q) iff Pp v Pq. The axiom says that for any two present-tensed propositions p and q, at some past time it was the case that p or q if and only if either at some past time it was the case that p or at some past time it was the case that q. The S4.3 system’s key axiom is the equivalence

Pp & Pq iff P(p & q) v P(p & Pq) v P(q & Pp).

This axiom captures part of our ordinary conception of time as a linear succession of states of the world. Another axiom might state that if proposition Q is true, then it will always be true that Q has been true at some time. Prior and others have suggested a wide variety of axioms for tense logic, but logicians still disagree about what axioms are needed to make correct beliefs about time be theorems that are logical consequences of those axioms. Some extension of classical tense logic is definitely needed in order to express “Q has been true for the past three days.”

The concept of being in the past is usually treated by metaphysicians as a predicate that assigns properties to events, but in this tense logic the concept is treated as an operator P upon propositions, and this difference in treatment is objectionable to some metaphysicians.

The other major approach to temporal logic does not use a tense logic. Instead, it formalizes temporal reasoning within a first-order logic without modal-like tense operators. This so-called method of “temporal arguments” adds an additional variable, a time argument, to any predicate involving time in order to indicate how its satisfaction depends on time. A predicate such as “is less than seven” does not involve time, but the predicate “is resting” does. If “x is resting” is represented classically as R(x), where R is a one-argument predicate, then it would be represented in temporal logic as R(x,t) and would be interpreted as saying x has property R at time t. R has been changed to a two-argument predicate by adding a “temporal argument.” The time variable “t” is treated as a new sort of variable with its own axioms. These axioms might allow time to be a dense linear ordering without endpoints, or to be even more like the real numbers.

Occasionally the method of temporal arguments uses a special constant symbol, say “n”, to denote now, the present time. This helps with the translation of common temporal statements. For example, the statement that Q has always been true may be translated into first-order temporal logic as

(∀t)[(t < n) → Q(t)].

Some temporal logics allow sentences to lack a classical truth value. The first person to give a clear presentation of the implications of treating declarative sentences as being neither true nor false was the Polish logician Jan Lukasiewicz in 1920. To carry out Aristotle’s suggestion that future contingent sentences do not yet have truth values, he developed a three-valued symbolic logic, with all grammatical declarative sentences having the truth-values of True, False, or else Indeterminate [T, F, or I]. Contingent sentences about the future, such as Aristotle’s prediction that there will be a sea battle tomorrow, are assigned an I. Truth tables for the connectives of propositional logic are redefined to maintain logical consistency and to maximally preserve our intuitions about truth and falsehood. See (Haack, 1974) for more details about this application of three-valued logic.


	Where history is becoming an experimental science
	Innovation and Excellence in Time Technology	The Official Site of the World Encyclopedia of Time, the Time Shop, and the Time Research Association.

Home \| About Us \| Educational Resources \| Encyclopedia \| The Time Shop \| Time Research Association \| Contact Us

	Contact the Anderson Institute The Anderson Institute UNITED STATES of AMERICA	Time Temporal Measurement Time Definition and Standards Religion and Time Philosophy and Time Physical Definition of Time Time Control Technologies	Time Travel Experiments in Time Perception of Time Culture and Time Art and Time Time Travel in Science Fiction Educational Resources
	Copyright © 1990-2012, The Anderson Institute is a trade name of Anderson Multinational LLC. All rights reserved.