The Anderson Institute Logo 
   Where history is becoming an experimental science      
Innovation and Excellence in Time Technology The Official Site of the World Encyclopedia of Time, the Time Shop, and the Time Research Association.    
   
  Home  |  About Us  |  Educational Resources  |  Encyclopedia  |  The Time Shop  |  Time Research Association  |  Contact Us

Physical Definition of Time

From the age of Newton up until Einstein's profound reinterpretation of the physical concepts associated with time and space, time was considered to be "absolute" and to flow "equably" (to use the words of Newton) for all observers. The science of classical mechanics is based on this Newtonian idea of time.

Einstein, in his special theory of relativity, postulated the constancy and finiteness of the speed of light for all observers. He showed that this postulate, together with a reasonable definition for what it means for two events to be simultaneous, requires that distances appear compressed and time intervals appear lengthened for events associated with objects in motion relative to an inertial observer.

Einstein showed that if time and space is measured using electromagnetic phenomena (like light bouncing between mirrors) then due to the constancy of the speed of light, time and space become mathematically entangled together in a certain way (called Minkowski space) which in turn results in Lorentz transformation and in entanglement of all other important derivative physical quantities (like energy, momentum, mass, force, etc) in a certain 4-vectorial way.

Classical Mechanics and Time
Time as part of Classical Mechanics
Classical mechanics

In classical mechanics, Newton's concept of "relative, apparent, and common time" can be used in the formulation of a prescription for the synchronization of clocks. Events seen by two different observers in motion relative to each other produce a mathematical concept of time that works pretty well for describing the everyday phenomena of most people's experience.

Modern physics

In the late nineteenth century, physicists encountered problems with the classical understanding of time, in connection with the behavior of electricity and magnetism. Einstein resolved these problems by invoking a method of synchronizing clocks using the constant, finite speed of light as the maximum signal velocity. This led directly to the result that observers in motion relative to one another will measure different elapsed times for the same event.

Two-dimensional spacetime depicted in three-dimensional spacetime
Two-Dimensional Spacetime Depicted in
Three-Dimensional Spacetime
Spacetime

Time has historically been closely related with space, the two together comprising spacetime in Einstein's special relativity and general relativity. According to these theories, the concept of time depends on the spatial reference frame of the observer, and the human perception as well as the measurement by instruments such as clocks are different for observers in relative motion. The past is the set of events that can send light signals to the observer, the future is the set of events to which the observer can send light signals.




Relativity of Simultaneity
Relativity of Simultaneity
Time dilation

"Time is nature's way of keeping everything from happening at once". This quote, attributed variously to Einstein, John Archibald Wheeler, and Woody Allen, says that time is what separates cause and effect. Einstein showed that people travelling at different speeds, while agreeing on cause and effect, will measure different time separations between events and can even observe different chronological orderings between non-causally related events. Though these effects are typically minute in the human experience, the effect becomes much more pronounced for objects moving at speeds approaching the speed of light. Many subatomic particles exist for only a fixed fraction of a second in a lab relatively at rest, but some that travel close to the speed of light can be measured to travel further and survive much longer than expected (a muon is one example). According to the special theory of relativity, in the high-speed particle's frame of reference, it exists, on the average, for a standard amount of time known as its mean lifetime, and the distance it travels in that time is zero, because its velocity is zero. Relative to a frame of reference at rest, time seems to "slow down" for the particle. Relative to the high-speed particle, distances seem to shorten. Even in Newtonian terms time may be considered the fourth dimension of motion; but Einstein showed how both temporal and spatial dimensions can be altered (or "warped") by high-speed motion.

Einstein (The Meaning of Relativity): "Two events taking place at the points A and B of a system K are simultaneous if they appear at the same instant when observed from the middle point, M, of the interval AB. Time is then defined as the ensemble of the indications of similar clocks, at rest relatively to K, which register the same simultaneously."

Einstein wrote in his book, Relativity, that simultaneity is also relative, i.e., two events that appear simultaneous to an observer in a particular inertial reference frame need not be judged as simultaneous by a second observer in a different inertial frame of reference.

Relativistic time versus Newtonian time

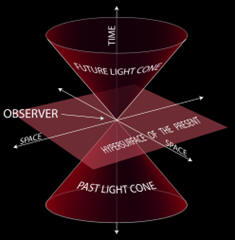
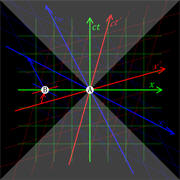
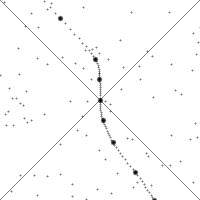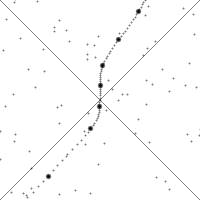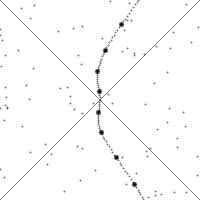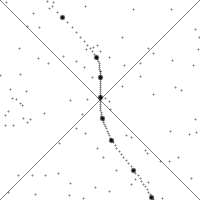
Views of Spacetime in a Relativistic Universe
Views of spacetime along the worldline of a
rapidly accelerating observer in a relativistic
universe.  The events ("dots") that pass the
two diagonal lines in the bottom half of the
image (the past light cone of the observer in
the origin) and the events visible to the
observer. 
The animations visualize the different treatments of time in the Newtonian and the relativistic descriptions. At heart of these differences are the Galilean and Lorentz transformations applicable in the Newtonian and relativistic theories, respectively.

In the figures, the vertical direction indicates time. The horizontal direction indicates distance (only one spatial dimension is taken into account), and the thick dashed curve is the spacetime trajectory ("world line") of the observer. The small dots indicate specific (past and future) events in spacetime.

The slope of the world line (deviation from being vertical) gives the relative velocity to the observer. Note how in both pictures the view of spacetime changes when the observer accelerates.

In the Newtonian description these changes are such that time is absolute: the movements of the observer do not influence whether an event occurs in the 'now' (i.e. whether an event passes the horizontal line through the observer).

However, in the relativistic description the observability of events is absolute: the movements of the observer do not influence whether an event passes the "light cone" of the observer. Notice that with the change from a Newtonian to a relativistic description, the concept of absolute time is no longer applicable: events move up-and-down in the figure depending on the acceleration of the observer.

Arrow of time

Time appears to have a direction – the past lies behind, fixed and incommutable, while the future lies ahead and is not necessarily fixed. Yet the majority of the laws of physics don't provide this arrow of time. The exceptions include the Second law of thermodynamics, which states that entropy must increase over time; the cosmological arrow of time, which points away from the Big Bang, and the radiative arrow of time, caused by light only traveling forwards in time. In particle physics, there is also the weak arrow of time, from CPT symmetry, and also measurement in quantum mechanics.

Quantized time

Time quantization is a hypothetical concept. In the modern established physical theories (the Standard Model of Particles and Interactions and General Relativity) time is not quantized.

Planck time (~ 5.4 × 10−44 seconds) is the unit of time in the system of natural units known as Planck units. Current established physical theories are believed to fail at this time scale, and many physicists expect that the Planck time might be the smallest unit of time that could ever be measured, even in principle. Tentative physical theories that describe this time scale exist; for instance loop quantum gravity.

Time and the Big Bang

Stephen Hawking in particular has addressed a connection between time and the Big Bang. In A Brief History of Time and elsewhere, Hawking says that even if time did not begin with the Big Bang and there were another time frame before the Big Bang, no information from events then would be accessible to us, and nothing that happened then would have any effect upon the present time-frame. Upon occasion, Hawking has stated that time actually began with the Big Bang, and that questions about what happened before the Big Bang are meaningless. This less-nuanced, but commonly repeated formulation has received criticisms from philosophers such as Aristotelian philosopher Mortimer J. Adler.

Scientists have come to some agreement on descriptions of events that happened 10−35 seconds after the Big Bang, but generally agree that descriptions about what happened before one Planck time (5 × 10−44 seconds) after the Big Bang will likely remain pure speculation.

Speculative physics beyond the Big Bang

While the Big Bang model is well established in cosmology, it is likely to be refined in the future. Little is known about the earliest moments of the universe's history. The Penrose-Hawking singularity theorems require the existence of a singularity at the beginning of cosmic time. However, these theorems assume that general relativity is correct, but general relativity must break down before the universe reaches the Planck temperature, and a correct treatment of quantum gravity may avoid the singularity.

There may also be parts of the universe well beyond what can be observed in principle. If inflation occurred this is likely, for exponential expansion would push large regions of space beyond our observable horizon.

Some proposals, each of which entails untested hypotheses, are:

w models including the Hartle-Hawking boundary condition in which the whole of space-time is finite; the Big Bang does represent the limit of time, but without the need for a singularity.

w brane cosmology models in which inflation is due to the movement of branes in string theory; the pre-big bang model; the ekpyrotic model, in which the Big Bang is the result of a collision between branes; and the cyclic model, a variant of the ekpyrotic model in which collisions occur periodically.

w chaotic inflation, in which inflation events start here and there in a random quantum-gravity foam, each leading to a bubble universe expanding from its own big bang.
Proposals in the last two categories see the Big Bang as an event in a much larger and older universe, or multiverse, and not the literal beginning.